Distribucion Normal Estandarizada
Summary
TLDREl script del video ofrece una explicación detallada de la distribución normal estandarizada y su aplicación en un ejemplo práctico. Se describe cómo, a partir de los tiempos de los primeros 75 corredores en el maratón de Londres 2012, se puede utilizar la media y la desviación estándar para estandarizar los valores y convertirlos en valores 'z'. Este proceso permite identificar qué porcentaje de corredores terminó el maratón en un tiempo específico, en este caso, en menos de 2 horas y 10 minutos. Utilizando la tabla de la distribución normal estandarizada o funciones de hoja de cálculo, se calcula que el 4% de los corredores cumplió esta condición. El video también menciona la posibilidad de calcular intervalos de tiempo utilizando valores 'z' correspondientes, lo cual se explorará en futuras secciones del video.
Takeaways
- 📊 La distribución normal estandarizada es una forma de transformar una distribución normal en una con una media de 0 y una desviación estándar de 1.
- 📈 El valor z indica cuántas desviaciones estándar un valor x se encuentra de la media y en qué dirección.
- ⏱️ En el ejemplo de los corredores del maratón de Londres 2012, la media de los tiempos fue de 8.300,4 segundos y la desviación estándar fue de 288,9 segundos.
- 📉 El 68% de los datos en una distribución normal están dentro de una desviación estándar de la media, el 95% están dentro de dos y el 99% dentro de tres.
- 🔍 Para estandarizar un valor x, se resta la media y se divide entre la desviación estándar, obteniendo el valor z.
- 📌 Los valores z negativos corresponden a valores x menores que la media, y los valores z positivos a valores x mayores que la media.
- 🧮 Para calcular el porcentaje de corredores que terminaron en menos de 2 horas y 10 minutos, se usó el valor z correspondiente a ese tiempo.
- 🔢 Se transformó 2 horas y 10 minutos en 7.800 segundos para calcular el valor z, que resultó en -1.75.
- 📉 Un valor z negativo indica que el tiempo se encuentra a la izquierda de la media en la distribución normal.
- 📊 La probabilidad de que un corredor haya terminado en menos de 2 horas y 10 minutos, con un valor z de -1.75, es del 4%.
- 📚 Se utilizó una tabla de distribución normal estandarizada y una hoja de cálculo para encontrar la probabilidad asociada al valor z.
- 📝 Tres corredores de los 75 analizados terminaron en menos de 2 horas y 10 minutos, lo que coincide con el porcentaje calculado.
Q & A
¿Qué es una distribución normal estandarizada?
-Una distribución normal estandarizada es una transformación de una distribución normal en una nueva variable con una media de 0 y una desviación estándar de 1. Esto se logra restando la media y dividiendo por la desviación estándar del valor original.
¿Cómo se calcula el valor z para un valor x en una distribución normal estandarizada?
-Para calcular el valor z, se resta la media del valor x y se divide entre la desviación estándar. Es decir, z = (x - media) / desviación estándar.
¿Cuál es el porcentaje de datos que se encuentra dentro de una desviación estándar de la media en una distribución normal?
-En una distribución normal, aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media.
¿Cuál es el porcentaje de corredores que realizó menos de 2 horas y 10 minutos en el maratón de Londres 2012 según la distribución normal estandarizada?
-Según la distribución normal estandarizada, el 4% de los corredores realizó menos de 2 horas y 10 minutos en el maratón de Londres 2012.
¿Cómo se puede convertir el tiempo de 2 horas y 10 minutos en segundos para su uso en cálculos?
-Para convertir 2 horas y 10 minutos en segundos, se multiplica 2 horas por 60 minutos por 60 segundos, sumando los 10 minutos multiplicados por 60 segundos, lo que da un total de 7800 segundos.
¿Cómo se determina el porcentaje de corredores que realizaron un tiempo específico utilizando la distribución normal estandarizada?
-Para determinar el porcentaje de corredores que realizaron un tiempo específico, se calcula el valor z para ese tiempo, luego se utiliza una tabla de distribución normal estandarizada o una función de hoja de cálculo para encontrar la probabilidad asociada a ese valor z, que corresponde al porcentaje de corredores.
¿Cuál es la desviación estándar de los tiempos de los primeros 75 corredores en el maratón de Londres 2012?
-La desviación estándar de los tiempos de los primeros 75 corredores en el maratón de Londres 2012 fue de 288.9 segundos.
¿Cómo se puede utilizar una hoja de cálculo para encontrar la probabilidad asociada a un valor z?
-En una hoja de cálculo, se puede utilizar la función de distribución normal estandarizada, como NORMSDIST en Excel, ingresando el valor z para encontrar la probabilidad asociada.
¿Cuál es la media de los tiempos de los primeros 75 corredores en el maratón de Londres 2012?
-La media de los tiempos de los primeros 75 corredores en el maratón de Londres 2012 fue de 8306.4 segundos.
¿Por qué es útil estandarizar una distribución normal?
-Estandarizar una distribución normal es útil porque transforma diferentes distribuciones normales en una escala común, lo que facilita comparaciones y análisis estadísticos entre diferentes conjuntos de datos.
¿Cómo se puede interpretar un valor z negativo en una distribución normal estandarizada?
-Un valor z negativo indica que el valor x se encuentra a una distancia de desviaciones estándar negativas de la media, es decir, se encuentra a la izquierda de la media en el gráfico de la distribución normal.
¿Cuál es la probabilidad de que un corredor haya terminado el maratón en más de 2 horas y 30 minutos si la media es de 8306.4 segundos y la desviación estándar es de 288.9 segundos?
-Para encontrar la probabilidad de que un corredor haya terminado en más de 2 horas y 30 minutos (equivale a 9000 segundos), se calcula el valor z para 9000 segundos y se utiliza una tabla de distribución normal estandarizada o una función de hoja de cálculo para encontrar la probabilidad a la derecha de ese valor z.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Distribución t student ejercicio resuelto (fácil)!!!!

Progresiones geométricas | Hallar el primer término |
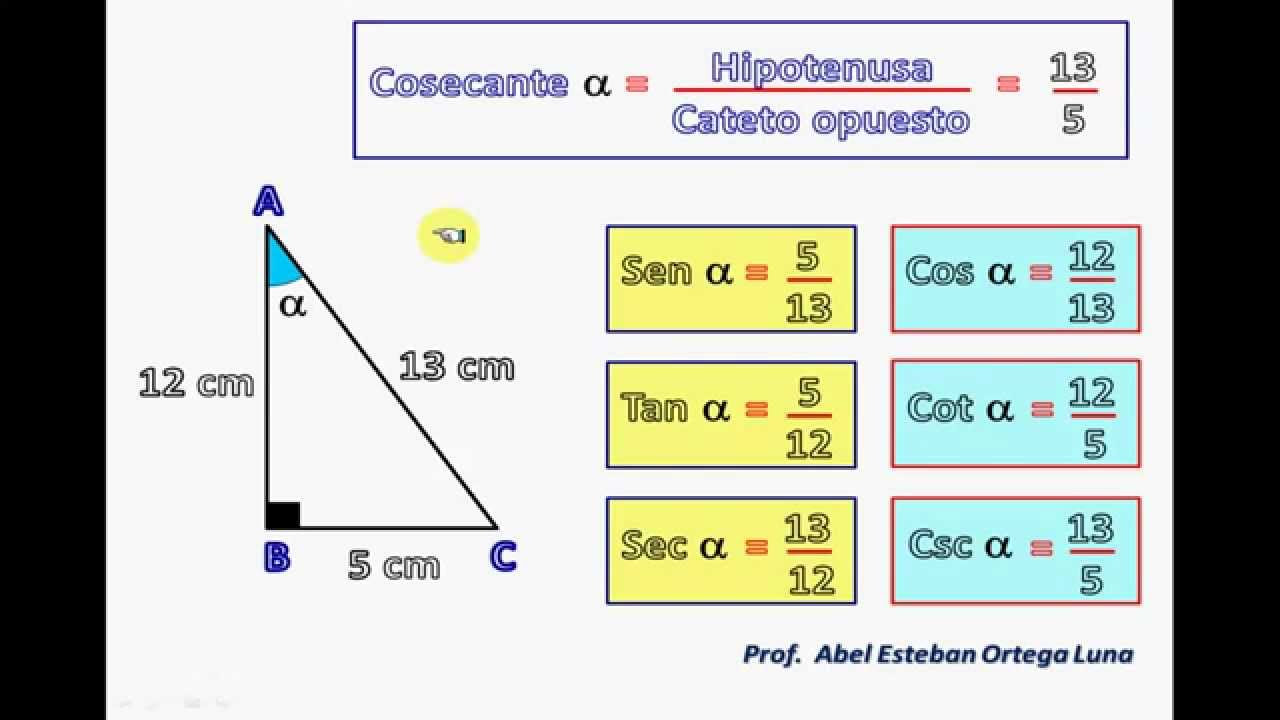
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Domina el Teorema del Límite Central: Qué es y por qué es tan Importante - Python

DISTRIBUIÇÃO NORMAL ESTATÍSTICA

Curso de Android con Java: Control Spinner con una lista de String
5.0 / 5 (0 votes)