How To Calculate The Interior Angles and Exterior Angles of a Regular Polygon
Summary
TLDRThis educational video explains how to calculate interior and exterior angles of regular polygons. It starts with a pentagon, detailing the formula for the sum of interior angles (180*(n-2)) and how to find each angle's measure. The video then demonstrates calculations for a hexagon and an octagon, reinforcing the concept with visual aids. It concludes by illustrating why the sum of exterior angles equals 360 degrees, using a full circle analogy.
Takeaways
- 🔢 The sum of interior angles of a regular polygon is calculated by the formula 180 × (n - 2), where n is the number of sides.
- 🤔 For a pentagon (n = 5), the sum of interior angles is 180 × (5 - 2) = 540 degrees.
- 📐 Each interior angle of a regular polygon is found by dividing the total sum by the number of sides.
- 📘 The measure of each interior angle of a pentagon is 540 ÷ 5 = 108 degrees.
- 🌐 The exterior angle of a regular polygon is supplementary to its interior angle, summing up to 180 degrees.
- 🔄 The measure of each exterior angle of a regular polygon is 360 ÷ n degrees.
- 🔵 For a pentagon, each exterior angle is 360 ÷ 5 = 72 degrees.
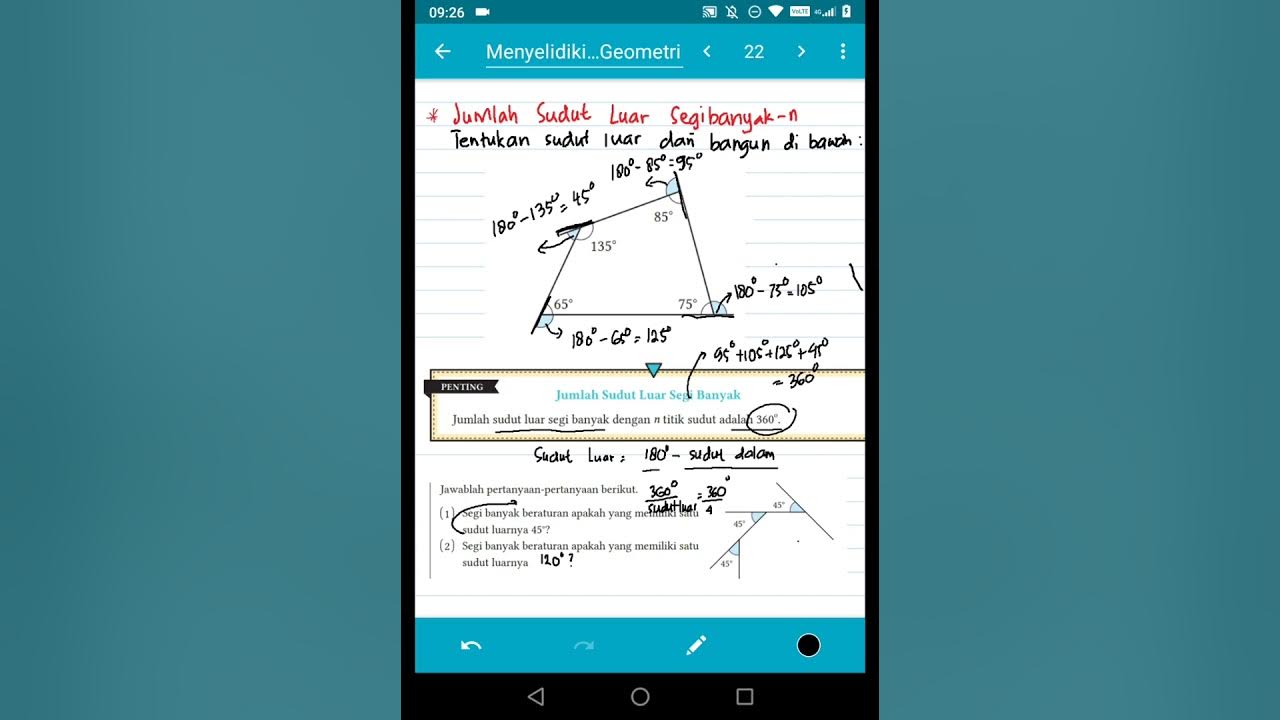
- 🐝 The sum of all exterior angles of any polygon is always 360 degrees, forming a full circle when connected.
- 🔑 The term 'Penta' means five, and similar prefixes indicate the number of sides for different polygons (e.g., 'Hexa' for six, 'Octa' for eight).
- 📈 For a hexagon (n = 6), the sum of interior angles is 180 × (6 - 2) = 720 degrees, and each interior angle is 720 ÷ 6 = 120 degrees.
- 🔲 For an octagon (n = 8), the sum of interior angles is 180 × (8 - 2) = 1080 degrees, and each interior angle is 1080 ÷ 8 = 135 degrees.
Q & A
What is the formula to calculate the sum of interior angles of a regular polygon?
-The formula to calculate the sum of interior angles of a regular polygon is 180 times (n - 2), where 'n' is the number of sides of the polygon.
How many sides does a pentagon have?
-A pentagon has five sides.
What is the sum of all interior angles of a regular pentagon?
-The sum of all interior angles of a regular pentagon is 540 degrees.
How do you find the measure of each interior angle of a regular pentagon?
-To find the measure of each interior angle of a regular pentagon, divide the sum of all interior angles (540 degrees) by the number of sides (5), which results in 108 degrees per angle.
What is the relationship between the interior and exterior angles of a polygon?
-The interior and exterior angles of a polygon form a linear pair and must add up to 180 degrees.
How can you calculate the measure of the exterior angle of a regular polygon?
-The measure of each exterior angle of a regular polygon can be calculated by either subtracting the measure of each interior angle from 180 degrees or by dividing 360 degrees by the number of sides (n) of the polygon.
What is the sum of all interior angles of a regular hexagon?
-The sum of all interior angles of a regular hexagon is 720 degrees.
How many degrees is each interior angle of a regular hexagon?
-Each interior angle of a regular hexagon measures 120 degrees.
What is the measure of each exterior angle of a regular hexagon?
-The measure of each exterior angle of a regular hexagon is 60 degrees.
How does the number of sides affect the sum of interior angles in a regular polygon?
-The sum of interior angles in a regular polygon increases with the number of sides, following the formula 180 times (n - 2), where 'n' is the number of sides.
Why is the sum of all exterior angles of any polygon always 360 degrees?
-The sum of all exterior angles of any polygon is always 360 degrees because if you draw one exterior angle at each vertex and connect them, they form a full circle, which has a total angle measurement of 360 degrees.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)