Interior and Exterior Angles of a Polygon
Summary
TLDRThis educational script explains the relationship between the interior and exterior angles of polygons. It highlights that the sum of interior angles in a triangle is 180 degrees and demonstrates how this sum increases with the number of sides in a polygon, using examples like squares, pentagons, and hexagons. The formula for calculating the sum of interior angles is presented as (n-2)*180, where 'n' is the number of sides. Additionally, it covers that the sum of exterior angles for any polygon is 360 degrees, and how to find the number of sides using the exterior angle. The script encourages viewers to practice these concepts with provided problems.
Takeaways
- 🔹 The interior angles of a triangle always sum up to 180 degrees.
- 🔹 A square, which is a quadrilateral, has interior angles summing to 360 degrees (2 x 180 degrees).
- 🔹 An irregular pentagon can be divided into three triangles, hence its interior angles sum to 540 degrees (3 x 180 degrees).
- 🔹 A hexagon can be divided into four triangles, with interior angles summing to 720 degrees (4 x 180 degrees).
- 🔹 The number of triangles that can fit inside a polygon is always two less than the number of its sides.
- 🔹 The formula to find the sum of the interior angles of any polygon is (n - 2) * 180 degrees, where 'n' is the number of sides.
- 🔹 The exterior angles of any polygon always sum up to 360 degrees.
- 🔹 The exterior angle of a polygon can be calculated by subtracting the interior angle from 180 degrees, using the fact that angles on a straight line sum to 180 degrees.
- 🔹 For a regular polygon, the number of sides can be determined by dividing 360 degrees by the measure of one exterior angle.
- 🔹 Each interior angle of a regular polygon can be calculated by dividing the sum of all interior angles by the number of sides.
Q & A
What is the sum of the interior angles of a triangle?
-The sum of the interior angles of a triangle is always 180 degrees.
How can you determine the sum of the interior angles of a square?
-Since a square can be divided into two triangles, the sum of its interior angles is two lots of 180 degrees, which equals 360 degrees.
What is the relationship between the number of triangles that can fit inside a polygon and the number of sides of the polygon?
-The number of triangles that can fit inside any polygon is always two less than the number of sides of the polygon.
How do you calculate the sum of the interior angles of a polygon given the number of sides?
-To find the sum of the interior angles of a polygon, you take the number of sides 'n', subtract two (to find how many triangles can fit inside), and then multiply by 180 degrees.
What is the sum of the exterior angles of any polygon?
-The sum of the exterior angles of any polygon is always 360 degrees.
How can you find the exterior angle of a polygon if you know the interior angle?
-If you know the interior angle, you can calculate the exterior angle by using the fact that angles on a straight line add up to 180 degrees.
For a regular polygon, how can you determine the number of sides using the exterior angle?
-For a regular polygon, you can find the number of sides by dividing 360 degrees by the measure of the exterior angle.
How can you calculate each interior angle of a polygon?
-You can calculate each interior angle of a polygon by dividing the sum of the interior angles by the number of angles or sides.
What is the significance of the number 180 degrees in the context of polygon angles?
-The number 180 degrees is significant because it represents the sum of the interior angles of a triangle, which is the building block for calculating the sum of interior angles of any polygon.
Can the formula for the sum of the interior angles be applied to irregular polygons?
-Yes, the formula for the sum of the interior angles can be applied to both regular and irregular polygons, as it is based on the number of sides and the geometric property that the sum of angles in a triangle is 180 degrees.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Interior and Exterior angles of polygons
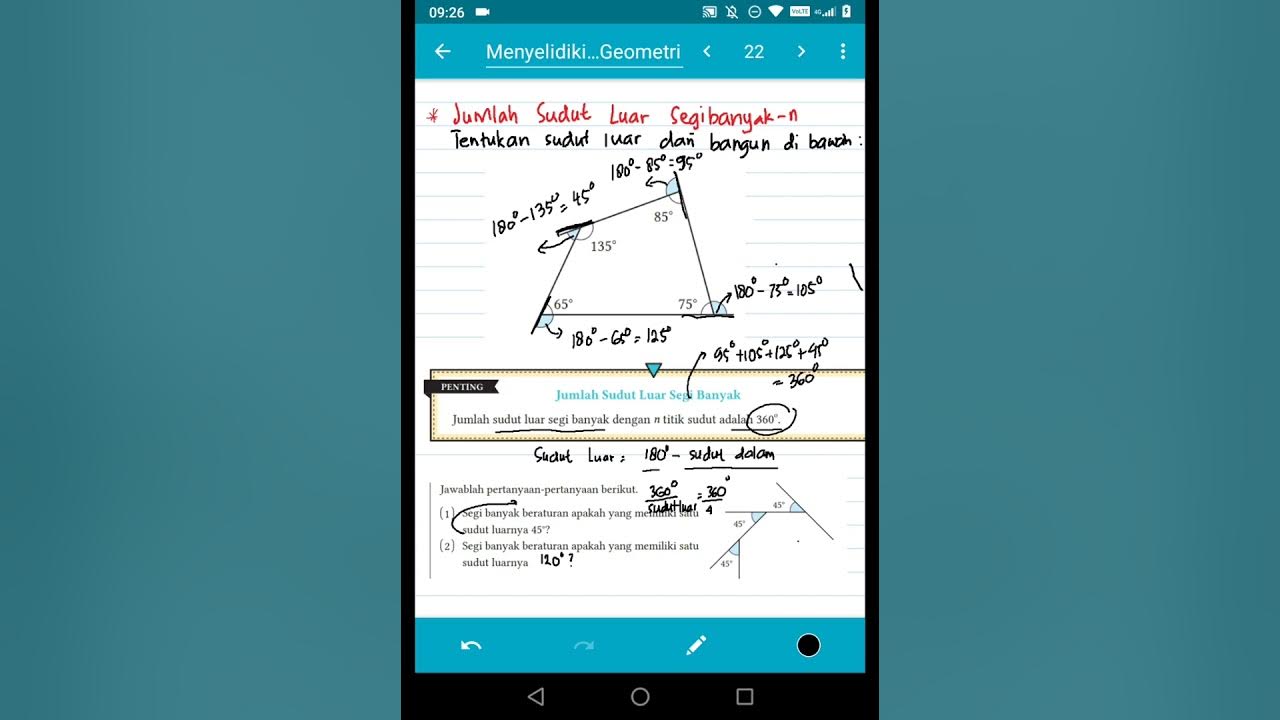
Sudut Luar Segibanyak-n
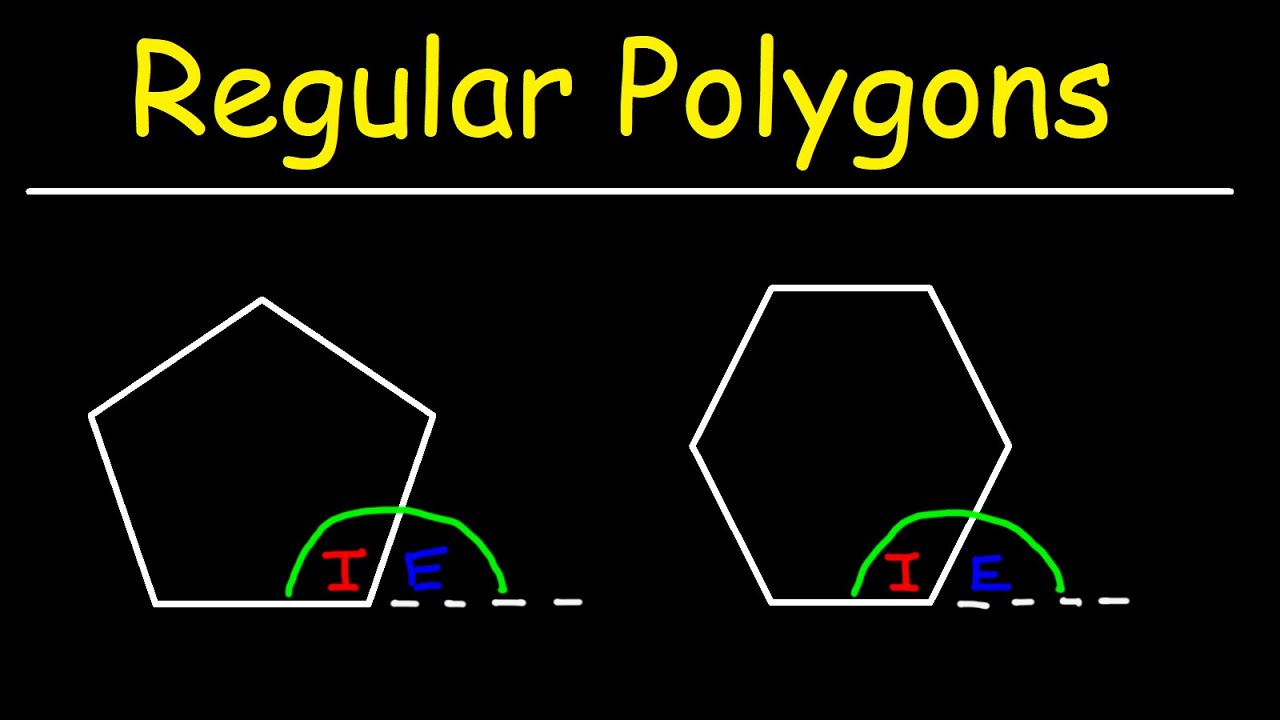
How To Calculate The Interior Angles and Exterior Angles of a Regular Polygon

Matematika Kelas 8 Bab 4 - Sudut Luar Segi Banyak - hal. 113 - 114 - Kurikulum Merdeka

Matematika Kelas 8 Bab 4 - Sudut Dalam Segi Banyak - hal. 110 - 112 - Kurikulum Merdeka

Garis dan Sudut (5) | Hubungan Antar Sudut pada Dua Garis Sejajar | Matematika Kelas 7
5.0 / 5 (0 votes)