Sudut Luar Segibanyak-n

Summary

In this lesson, the teacher explains the concept of exterior angles in polygons, focusing on how to calculate them and their relationship to interior angles. By subtracting the interior angle from 180°, students learn how to find the exterior angles. The sum of all exterior angles in any polygon is always 360°. The lesson also includes exercises to calculate exterior angles, determine the number of sides in a regular polygon, and verify the sum of exterior angles. The teacher emphasizes understanding these principles through practical examples and problems.

Takeaways

• 😀 The lesson focuses on exterior angles in polygons, contrasting them with interior angles.
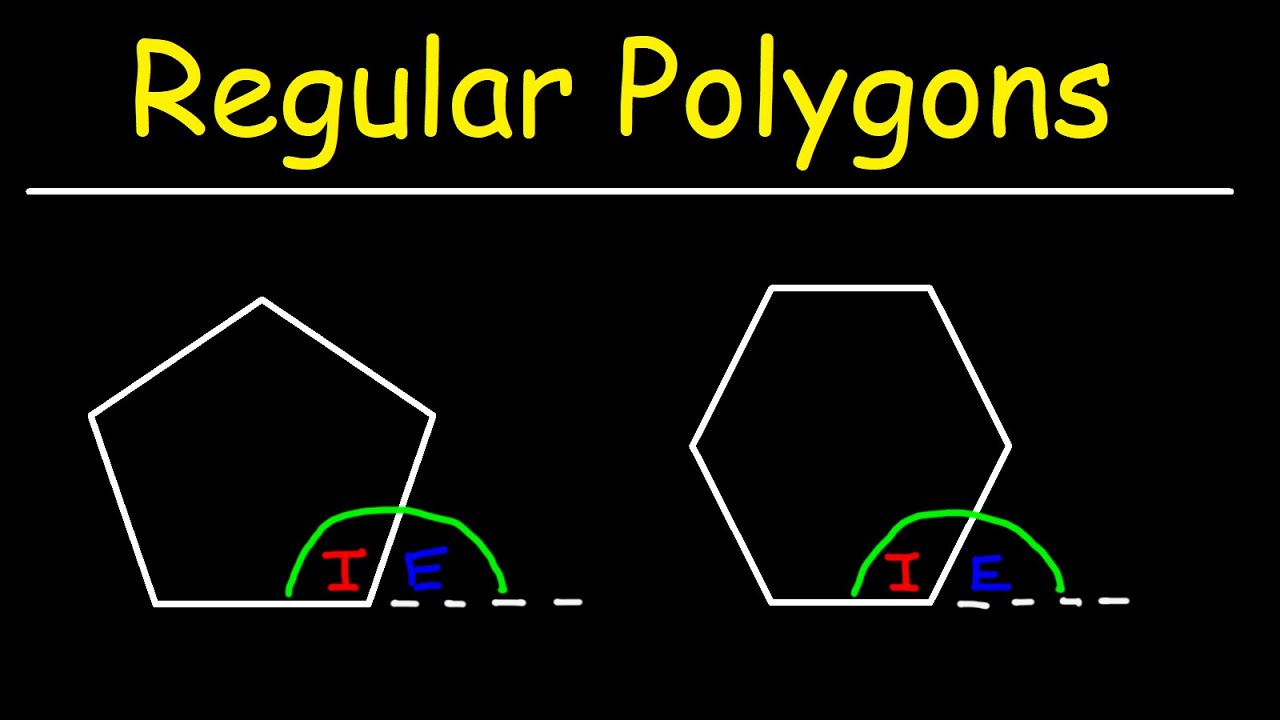
• 😀 The exterior angle of a polygon is the angle formed outside the polygon at any of its vertices.
• 😀 The sum of all exterior angles of any polygon is always 360 degrees.
• 😀 To find an exterior angle of a regular polygon, divide 360 degrees by the number of sides (n).
• 😀 For irregular polygons, exterior angles can be calculated by subtracting the interior angle from 180 degrees.
• 😀 Example calculation: if the interior angle is 85 degrees, the exterior angle is 180 - 85 = 95 degrees.
• 😀 The instructor emphasizes practicing calculations of exterior angles using specific examples from irregular polygons.
• 😀 For a regular polygon, the formula for the sum of interior angles is (n - 2) * 180 degrees.
• 😀 The lesson provides exercises that help students apply the exterior and interior angle formulas to solve problems.
• 😀 The total of all exterior angles of a polygon with 'n' sides is always 360 degrees, regardless of the polygon's regularity.
• 😀 In a regular polygon, if the exterior angle is known, the number of sides (n) can be determined by dividing 360 by the exterior angle.

Q & A

What is the main focus of the lesson discussed in the transcript?

The lesson focuses on understanding exterior angles (sudut luar) in polygons and how to calculate them, as well as discussing the sum of exterior angles in various polygon types.

How are exterior angles defined in the context of polygons?

Exterior angles are angles formed outside a polygon when one side is extended. They are supplementary to the adjacent interior angles of the polygon.

How do you calculate the exterior angle of a polygon?

To calculate an exterior angle of a polygon, subtract the interior angle from 180 degrees, as they are supplementary (sum to 180°).

What is the formula for calculating the sum of the interior angles of a polygon with 'n' sides?

The sum of the interior angles of an 'n'-sided polygon is given by the formula: (n - 2) × 180°.

What is the total sum of exterior angles for any polygon, regardless of the number of sides?

The total sum of the exterior angles of any polygon is always 360°, regardless of the number of sides.

What is the method to find the number of sides of a regular polygon if the exterior angle is known?

To find the number of sides of a regular polygon, divide 360° by the measure of one exterior angle. For example, if the exterior angle is 45°, the number of sides would be 360 ÷ 45 = 8.

In the example, if the exterior angle is 120°, how many sides does the polygon have?

If the exterior angle is 120°, divide 360° by 120°, resulting in 3 sides. Therefore, the polygon is a triangle.

What should students do if they need a refresher on how to calculate the angles?

Students should review the video lesson from the previous session, as it covers the necessary steps and examples for calculating interior and exterior angles.

What is the significance of the supplementary angles in the calculation of exterior angles?

The significance is that exterior angles and their adjacent interior angles always add up to 180°, allowing us to calculate the exterior angle by subtracting the interior angle from 180°.

What does the lesson suggest when a student is unsure about a calculation or concept?

The lesson encourages students to ask questions during the Zoom session for clarification if they do not understand a specific concept or calculation.