Angles in Polygons

Summary

This video explains the properties of polygons, focusing on shapes with 3 to 6 sides (triangle, quadrilateral, pentagon, and hexagon). It covers regular and irregular polygons, demonstrating how regular shapes have equal sides and angles. The video explores the angle sums for each polygon and the method for calculating them, introducing the formula (n-2) × 180°. The concept of exterior angles is also discussed, emphasizing how they always add up to 360°. Examples and exercises guide viewers in calculating angles for various polygons, making geometry accessible and engaging.

Takeaways

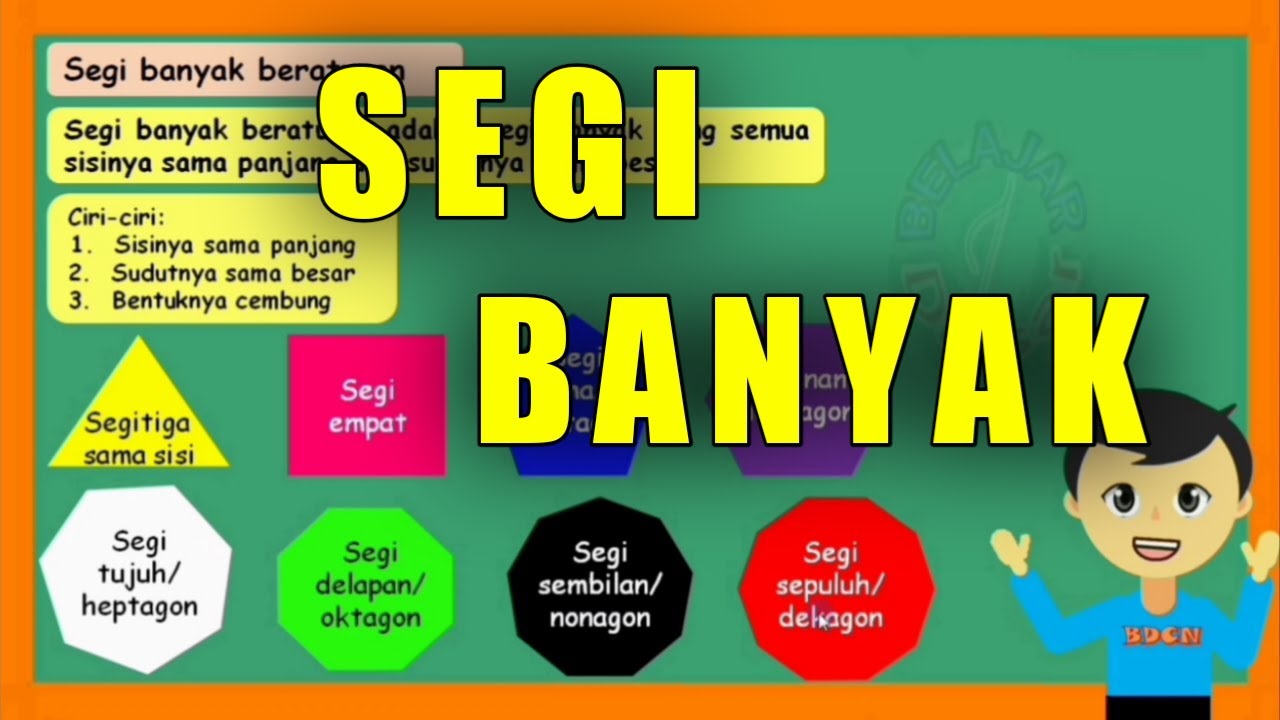
• 😀 A polygon is a 2D shape with straight sides, and common examples include triangles, quadrilaterals, pentagons, and hexagons.
• 😀 Regular polygons have equal sides and equal angles, while irregular polygons have sides and angles that are not equal.
• 😀 The sum of interior angles for a triangle is 180°, for a quadrilateral is 360°, for a pentagon is 540°, and for a hexagon is 720°.
• 😀 To calculate the angle sum of any polygon, use the formula (n - 2) * 180, where 'n' is the number of sides.
• 😀 For regular polygons, each interior angle is found by dividing the angle sum by the number of sides.
• 😀 Exterior angles of polygons always add up to 360°, and each exterior angle can be found by dividing 360° by the number of sides.
• 😀 For a regular hexagon (6 sides), each exterior angle is 60°, and for a regular dodecagon (12 sides), each exterior angle is 30°.
• 😀 The exterior and interior angles of a polygon are supplementary, meaning their sum is always 180°.
• 😀 To find the number of sides of a polygon based on its exterior angle, divide 360° by the exterior angle.
• 😀 In irregular polygons, missing angles can be found by subtracting the sum of known angles from the total angle sum, using the formula (n - 2) * 180.

Q & A

What is the difference between regular and irregular polygons?

A regular polygon has all sides and angles equal, while an irregular polygon does not have equal sides or angles.

How do you calculate the sum of interior angles in a polygon?

To calculate the sum of interior angles of a polygon, use the formula: (n - 2) * 180, where 'n' is the number of sides of the polygon.

What is the sum of the interior angles of a pentagon?

The sum of the interior angles of a pentagon is 540 degrees, as a pentagon can be divided into three triangles, and each triangle's angles sum to 180 degrees.

How do you calculate the size of each interior angle in a regular polygon?

For a regular polygon, divide the sum of the interior angles by the number of sides. For example, in a regular pentagon, divide 540 degrees by 5 to get 108 degrees per angle.

How can you find the exterior angle of a polygon?

The exterior angle of a polygon can be found by dividing 360 degrees by the number of sides (n). For example, the exterior angle of a regular hexagon is 360 ÷ 6 = 60 degrees.

What is the relationship between interior and exterior angles?

Interior and exterior angles of a polygon are supplementary, meaning they add up to 180 degrees.

If a polygon has 12 sides, what is the size of each exterior angle?

For a regular 12-sided polygon (dodecagon), the exterior angle is 360 ÷ 12 = 30 degrees.

What is the formula to find the number of sides in a polygon if you know the size of the exterior angle?

To find the number of sides (n) in a polygon, divide 360 by the size of the exterior angle. For example, if the exterior angle is 30 degrees, the polygon has 360 ÷ 30 = 12 sides.

How do you calculate the missing interior angle in an irregular polygon?

To calculate the missing interior angle in an irregular polygon, first calculate the sum of all angles using the formula (n - 2) * 180. Then, subtract the sum of the known angles from the total to find the missing angle.

How do you calculate the exterior angle of a polygon with 8 sides?

For an 8-sided polygon (octagon), divide 360 by 8 to get 45 degrees as the exterior angle.