Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
Summary
TLDRJohn Barron presents recent advancements in computer vision and graphics using multi-layer perceptrons (MLPs) to represent 3D objects and scenes. MLPs can output complex functions in low-dimensional domains, but they struggle with high-frequency details. The solution introduced is a Fourier feature mapping technique, which transforms input coordinates into sinusoids, enabling the MLP to recover fine details. This technique is effective in low-dimensional tasks, like 3D shape representation and neural radiance fields, outperforming standard MLPs. It balances high-frequency representation and smoothness, avoiding overfitting while solving a variety of inverse problems.
Takeaways
- 🧑🏫 The presentation is led by John Barron, representing his collaborators.
- 🔄 Recent progress in computer vision and graphics involves using fully connected networks, also known as multi-layer perceptrons (MLPs), to represent 3D objects or scenes.
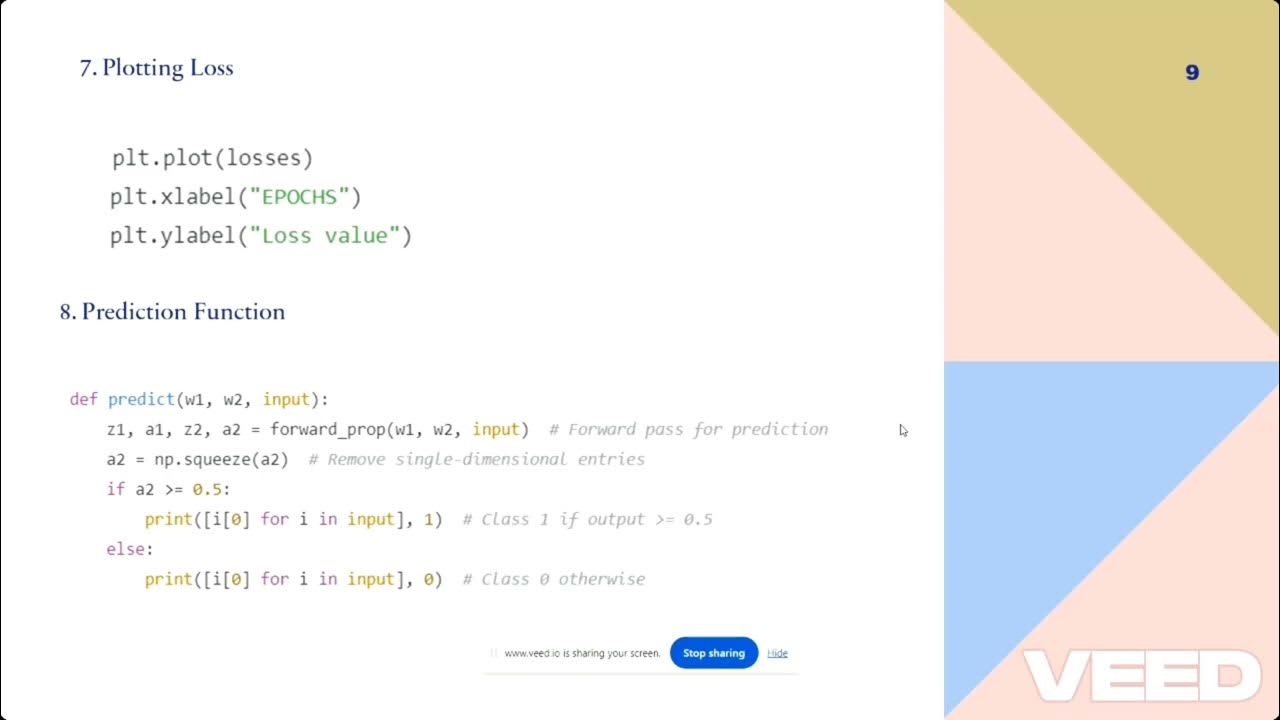
- 🧠 MLPs take low-dimensional inputs, such as 3D coordinates, and output binary values, helping to identify if a point is inside or outside a 3D object.
- 🔍 MLPs offer continuous representations, allowing for dense sampling and shape recovery.
- 📊 Unlike typical neural networks that deal with high-dimensional inputs (e.g., pixels in an image), MLPs can represent complex functions on low-dimensional domains.
- 🌈 A simple MLP can represent an image by taking a 2D pixel coordinate as input and outputting an RGB color, but it struggles to capture high-frequency details.
- ⚠️ This high-frequency detail problem appears in other domains too, such as 1D curves and 3D shapes.
- ✨ The solution proposed involves passing the input coordinates through a Fourier feature mapping, using randomly scaled and rotated sinusoids to control frequencies.
- 📈 Using Fourier feature inputs helps MLPs capture fine high-frequency details and perform better interpolation between data points.
- 📉 While increasing the frequency of Fourier features improves fitting, excessively high frequencies lead to overfitting.
Q & A
What are MLPs and how are they used in this context?
-MLPs, or multi-layer perceptrons, are simple fully connected networks used to represent 3D objects or scenes by taking in low-dimensional inputs like 3D coordinates and outputting values such as whether a point lies inside or outside a 3D object.
Why are MLPs considered continuous representations?
-MLPs are continuous representations because they can be densely sampled to recover the encoded shape of an object, which allows for smooth and continuous output, unlike discrete representations.
What is a key challenge when using MLPs to represent images?
-A key challenge is that MLPs struggle to capture high-frequency details in images, even when the network has more weights than the number of pixels in the image.
How does the problem with high-frequency detail representation manifest in MLPs?
-When training MLPs on tasks such as representing 2D images, 1D curves, or 3D shapes, they often produce oversmoothed results, failing to accurately recover fine high-frequency details.
What solution is presented in the video to address the high-frequency detail issue?
-The proposed solution involves passing the input coordinates through a Fourier feature mapping, which applies randomly scaled and rotated sinusoids to the input, enabling MLPs to capture high-frequency details more effectively.
How does the Fourier feature mapping improve MLP performance?
-Fourier feature mapping controls the frequencies that the MLP can represent, allowing it to interpolate more finely between training data points and recover high-frequency details.
What theoretical tools are used to explain the effect of Fourier features?
-The neural tangent kernel theory is used to explain that Fourier feature inputs cause MLPs to interpolate between data points, with the frequencies of the sinusoids directly affecting the smoothness of the interpolation kernel.
Why is smoothness beneficial in typical neural network applications, but a problem here?
-In typical applications, smoothness helps prevent overfitting by producing generalized functions, which is beneficial for tasks like classification. However, in this context, smoothness prevents MLPs from capturing high-frequency details needed for tasks such as 3D shape representation.
What happens when the frequencies of the Fourier feature mapping are increased?
-Increasing the frequencies allows the MLP to better fit the training points and capture more details. However, if the frequencies are increased too much, the MLP can overfit the data, leading to poor generalization.
What are some practical applications of this Fourier feature technique?
-This technique can be applied to a wide range of low-dimensional problems, such as representing 3D shapes, solving inverse imaging problems like MRI reconstruction, and reconstructing neural radiance fields from images.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)