02. Integral of a constant function
Summary
TLDREn este video, el presentador resuelve una integral básica, explicando el proceso paso a paso. Comienza mostrando cómo la integral de dx sobre 7 puede escribirse como la integral de 1/7 dx. Luego, aplica la propiedad de las constantes fuera de la integral y resuelve la integral de dx, que da como resultado 'x' más una constante. El video ofrece una breve introducción a este tipo de integrales y recomienda a los espectadores revisar un video anterior para comprender mejor los conceptos. Además, invita a los usuarios a intentar resolver una integral similar por su cuenta.
Takeaways
- 😀 El video es parte de una serie educativa sobre resolución de integrales en matemáticas.
- 😀 La integral presentada se muestra como una fracción con 1 en el numerador y 7 en el denominador.
- 😀 Se menciona que la integral de dx sobre 7 se puede escribir también como 1/7 de la integral de dx.
- 😀 La propiedad de las constantes en integrales se aplica: la constante se puede sacar fuera de la integral.
- 😀 Al aplicar esta propiedad, el factor 1/7 se coloca fuera de la integral y se resuelve la integral de dx.
- 😀 La integral de dx es simplemente x, según la regla básica de integrales.
- 😀 Después de realizar la integral, se debe añadir una constante al resultado, como se explica en el video anterior.
- 😀 Se recomienda revisar el video anterior para una comprensión más detallada de las constantes en integrales.
- 😀 El resultado final de la integral es (1/7) * x + C, donde C es la constante de integración.
- 😀 El video invita a los estudiantes a intentar resolver una integral similar por su cuenta antes de que se resuelva en un próximo video.
Q & A
¿Cómo se resuelve la integral de dx sobre 7?
-La integral de dx sobre 7 se resuelve sacando la constante 1/7 fuera de la integral, lo que deja la integral de dx, que es simplemente x. Luego se suma una constante de integración, C.
¿Por qué se puede sacar la constante 1/7 fuera de la integral?
-Según una propiedad de las integrales, cualquier constante multiplicando a la función dentro de la integral puede sacarse fuera de ella sin afectar el resultado de la integración.
¿Qué representa la constante de integración que se suma al final?
-La constante de integración, denotada como C, es necesaria porque la integral de una función puede tener múltiples soluciones que se diferencian solo por una constante.
¿Qué se debe hacer después de realizar una integral, según el video?
-Después de realizar una integral, siempre se debe agregar una constante de integración C al resultado, como se explica en el video.
¿Qué significa la notación 'dx' en la integral?
-La notación 'dx' indica que la variable de integración es x, es decir, que estamos integrando con respecto a x.
¿Cómo se llama la propiedad que permite sacar una constante fuera de la integral?
-La propiedad que permite sacar una constante fuera de la integral se conoce como la propiedad de linealidad de las integrales.
¿Por qué el resultado de la integral de dx es simplemente x?
-La integral de dx es una de las integrales más simples, ya que la derivada de x con respecto a x es 1, por lo que la integral de 1 con respecto a x es x.
¿Qué consejo ofrece el instructor al final del video?
-El instructor sugiere que si no han visto el video anterior, lo hagan antes de seguir con este, ya que proporciona una base importante para comprender mejor el tema.
¿En qué se diferencia esta integral de la que se resolvió en el video anterior?
-La integral resuelta en este video es muy similar a la del video anterior, pero en este caso se trata de una constante multiplicada por la variable dx, lo que requiere la aplicación de propiedades de linealidad.
¿Qué debe hacer un estudiante si no comprende la resolución de esta integral?
-Si un estudiante no comprende la resolución de esta integral, el instructor recomienda revisar el video anterior para entender mejor el proceso y los conceptos involucrados.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Razón de Cambio Promedio Ejercicios resueltos #01| Explicado Paso a Paso

11. Integral de raíz cúbica de x (potencia fraccionaria)
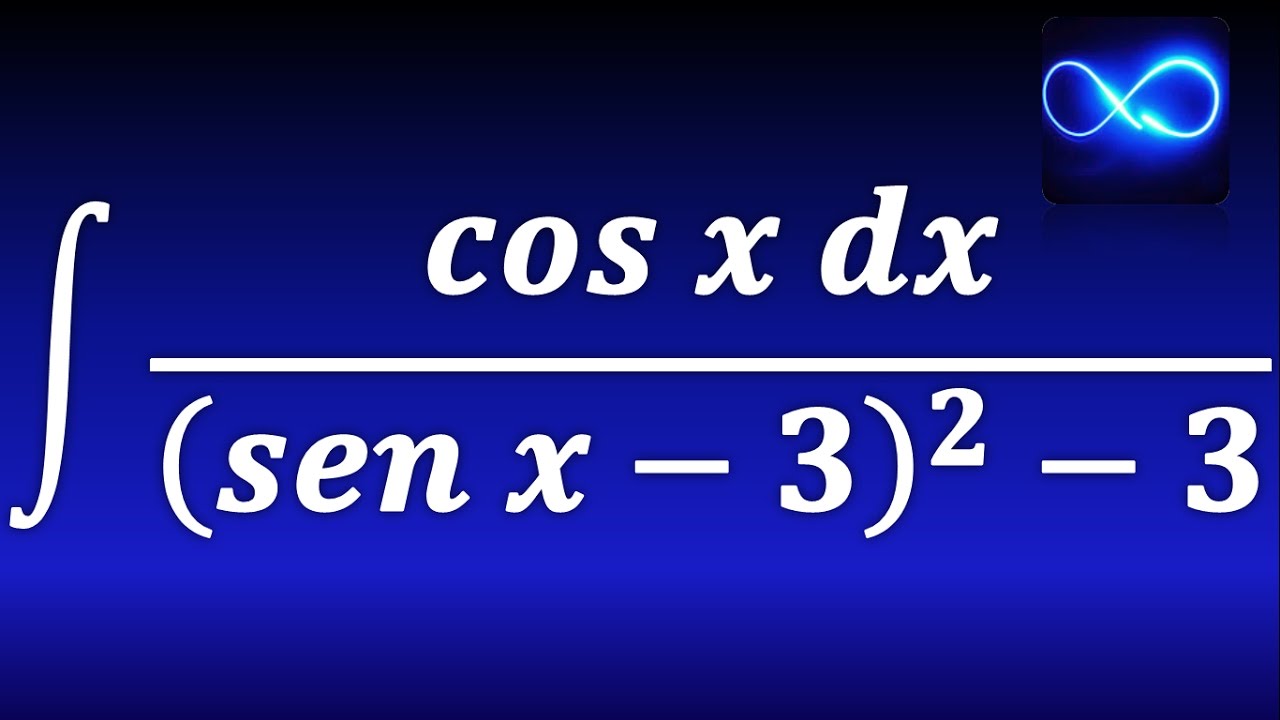
Integral de coseno entre seno cuadrado menos 3

118. Integración por partes, x por coseno (Algebraica por trigonométrica) (Ejemplo resuelto)

Teorema de Pitágoras | Ejercicio de práctica

MOLE POBLANO DESDE CERO | ALE DE NAVA
5.0 / 5 (0 votes)
