118. Integración por partes, x por coseno (Algebraica por trigonométrica) (Ejemplo resuelto)
Summary
TLDREn este video de Mate Fácil, se resuelve una integral de x * coseno de x usando el método de integración por partes. Se explica cómo elegir la función u y db siguiendo la regla LIATE, y se detalla el proceso paso a paso. El resultado final es x * seno de x + coseno de x + C. El video invita a los espectadores a intentar resolver la integral de x * e^x antes del próximo video y los anima a dejar preguntas o sugerencias en los comentarios. Además, se pide apoyo a través de 'likes' y compartir el contenido.
Takeaways
- 📘 El video enseña cómo calcular la integral de x * coseno(x) * dx utilizando el método de integración por partes.
- 🔑 Se utiliza la fórmula de integración por partes: ∫u dv = uv - ∫v du para resolver la integral.
- 📚 Se elige 'x' como la función 'u' y 'coseno(x)' como 'dv' siguiendo la regla de LIATE (Logaritmos, Inversas, Algebraicas, Trigonometricas, Exponenciales).
- 🧮 La derivada de 'u' (x) es 1, por lo que 'du' es dx.
- 📐 La integral de 'dv' (coseno(x)) es 'seno(x)', lo que se convierte en 'v'.
- ✅ Se aplica la fórmula de integración por partes y se obtiene x * seno(x) - ∫seno(x) dx.
- 🔄 Se calcula la integral de 'seno(x)', que es -coseno(x), y se sustituye en la fórmula.
- 📉 El resultado final de la integral es x * seno(x) + coseno(x) + C, donde C es la constante de integración.
- 🎥 Se invita a los espectadores a intentar resolver el próximo desafío de integrar x * e^x * dx antes de ver el siguiente video.
- 👍 Se anima a los espectadores a dar like, compartir y comentar sus dudas o sugerencias en el canal.
Q & A
¿Cuál es la fórmula utilizada para resolver la integral por partes?
-La fórmula utilizada es: la integral de u * dv es igual a u * v menos la integral de v * du.
¿Qué es lo primero que se debe hacer al aplicar la regla de integración por partes?
-Lo primero es elegir las funciones u y dv de la integral original. En este caso, hay que seleccionar cuál función será u y cuál dv.
¿Qué regla se utiliza para seleccionar la función u en la integración por partes?
-Se utiliza la regla LIATE, que indica el orden en que se deben elegir las funciones para u: Logarítmica, Inversa, Algebraica, Trigonométrica y Exponencial.
¿Qué función se selecciona como u en este caso y por qué?
-Se selecciona la función algebraica, que es x, porque según la regla LIATE, las funciones algebraicas tienen prioridad sobre las trigonométricas.
¿Qué función se selecciona como dv y por qué?
-La función dv es lo que sobra de la integral original, que en este caso es coseno de X * dx.
¿Cómo se obtiene du a partir de u?
-du se obtiene derivando u, es decir, la derivada de x es 1, por lo que du es 1 * dx.
¿Cómo se obtiene v a partir de dv?
-v se obtiene integrando dv. La integral de coseno de X es seno de X.
¿Cuál es el resultado intermedio antes de resolver la segunda integral?
-El resultado intermedio es: x * seno de X menos la integral de seno de X * dx.
¿Cuál es el resultado de la integral de seno de X?
-La integral de seno de X es -coseno de X.
¿Cuál es el resultado final de la integral?
-El resultado final es: x * seno de X + coseno de X + la constante de integración.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Integración por partes ejemplo 2 | Cálculo integral - Vitual

Técnicas de integración | Integración por partes
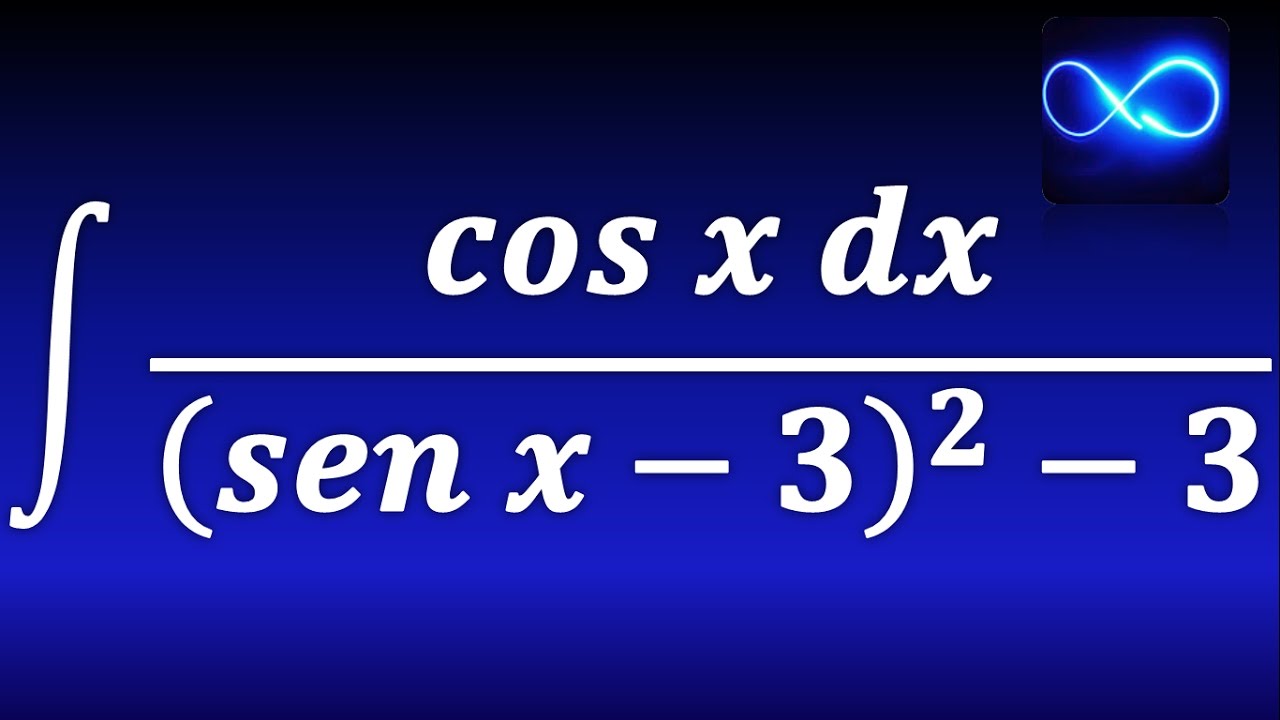
Integral de coseno entre seno cuadrado menos 3

INTEGRACIÓN por PARTES | Integrales Cíclicas

50. Integral indefinida por el método de Sustitución (Cambio Variable). Expresión con raíz cuadrada.

08. Límite con indeterminación 0/0
5.0 / 5 (0 votes)
