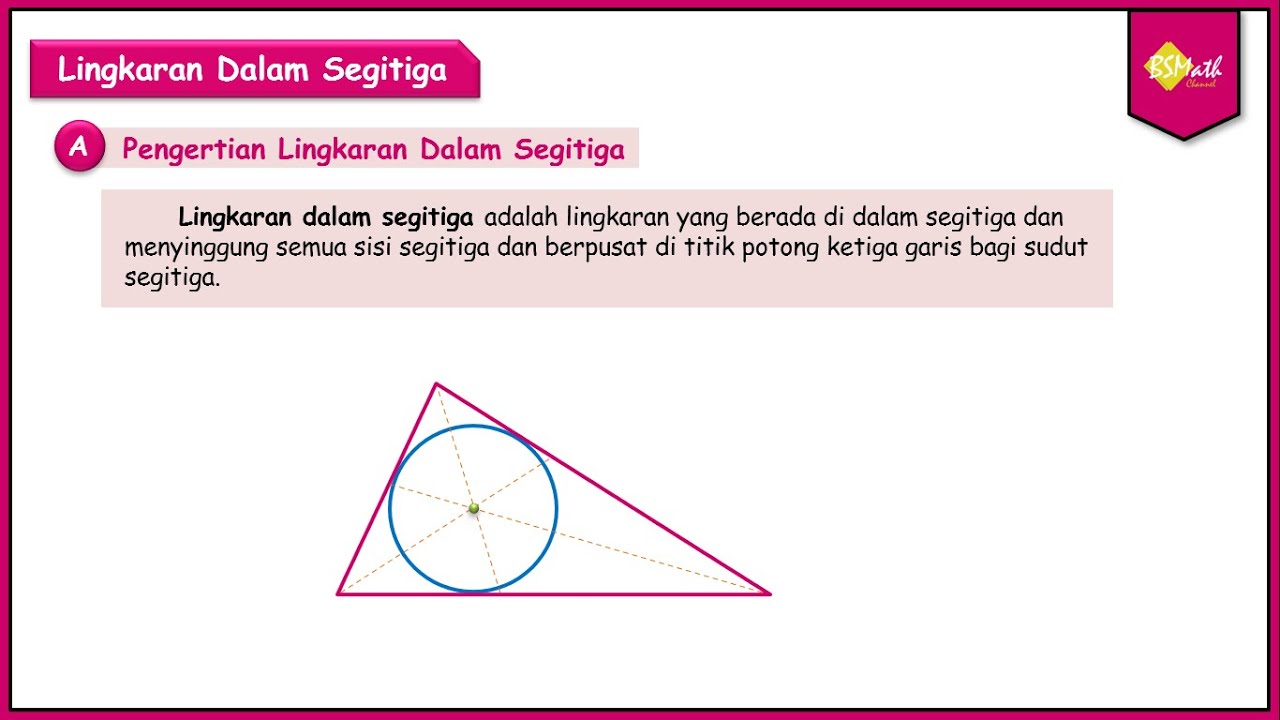
Sierpinski Arrowhead Curve L-system (118098 steps!)
Summary
TLDRIn this video, the process of approximating the Serinsky Triangle is explored using a Lindenmayer system (L-system) and Turtle Graphics. The L-system starts with a string, applying production rules to generate more complex strings at each stage. These strings are then interpreted to move on a plane, creating geometric patterns. The video demonstrates how, after several iterations, the final string produces a shape that approximates the Serinsky Triangle. The explanation includes step-by-step guidance on the string generation, movement rules, and the visual results created through this Turtle Graphics process.
Takeaways
- 😀 An L-system (Lindenmayer system) is used to generate a fractal-like shape in the plane.
- 😀 The process begins with an initial string 'A', and specific production rules are applied to it over several iterations.
- 😀 The production rules for 'A' and 'B' are: A → B-A-B and B → A+B+A.
- 😀 Dashes (-) and plus signs (+) are used to represent rotations, with '-' rotating 60° clockwise and '+' rotating 60° counterclockwise.
- 😀 The turtle graphics method is employed, where 'A' and 'B' represent forward movements, and '+' and '-' control rotations.
- 😀 After each iteration, the string becomes more complex, and the resulting string is used to guide the movement of the turtle on the plane.
- 😀 The video demonstrates how the string evolves through several iterations, including the 10th iteration in the example.
- 😀 The L-system process can be repeated indefinitely, creating increasingly intricate patterns.
- 😀 The final shape formed by the turtle graphics after applying 10 iterations reveals a visually striking fractal structure.
- 😀 The technique offers a fascinating way to approximate shapes like the Sierpinski Triangle using simple string rules and turtle graphics.
- 😀 The video encourages viewers to explore other L-system-based shapes and fractals, with links to additional resources provided.
Q & A
What is the main concept being discussed in the video?
-The video discusses approximating the Sierpinski triangle using a Lindenmayer system (L-system) with a single curve on a plane, combined with Turtle Graphics for visualization.
What are the initial production rules in the Lindenmayer system for this process?
-The initial production rules replace the character 'A' with 'B-A' and the character 'B' with 'A+B+A'. Dashes and pluses remain unchanged at each iteration.
What happens in the first stage of the process?
-In the first stage, the string 'A' is replaced with 'B-A'.
How does the string evolve in the second stage of the process?
-In the second stage, the string 'B-A' becomes 'A+B+A-B-A'.
How is the string used to walk on the plane?
-Each character in the string is interpreted as follows: 'A' or 'B' means stepping one unit forward, '+' means rotating 60° to the left, and '-' means rotating 60° to the right.
What happens after applying the production rules repeatedly?
-As the production rules are applied repeatedly, the string grows, and its resulting pattern forms a fractal shape, approximating the Sierpinski triangle.
What does the string look like after the 10th iteration of the production rules?
-After the 10th iteration, the string is a complex combination of characters, which is then used to draw a fractal shape on the plane using Turtle Graphics.
What is the significance of the '+' and '-' symbols in the process?
-The '+' and '-' symbols are used to control the rotation of the drawing process, with '+' rotating 60° left and '-' rotating 60° right, guiding the formation of the fractal.
What role does Turtle Graphics play in this process?
-Turtle Graphics is used to visually plot the path on the plane by interpreting the string produced from the L-system. It enables the creation of the fractal shape by following the instructions encoded in the string.
Why is the Sierpinski triangle an interesting shape to generate with this method?
-The Sierpinski triangle is a classic fractal with self-similarity, meaning that each iteration creates smaller versions of the whole shape, making it an ideal candidate to demonstrate the recursive nature of L-systems and Turtle Graphics.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)