Module05Video01

Summary

In this video, the process of modeling a TV adjustment and inspection system using queuing theory is explored. The video covers constructing a standard tandem queuing model, considering the impact of reentrant flow when TVs fail inspection and return for readjustment. It also delves into using selection weights for routing entities probabilistically and validating the model using simulation. The video further examines the use of reference properties for comparing different processing time distributions, ultimately verifying the model’s behavior against expectations and highlighting key performance metrics like utilization and time in the system.

Takeaways

• 😀 The video explains how to model a TV adjustment inspection facility using queuing theory and selection weights in Simio.
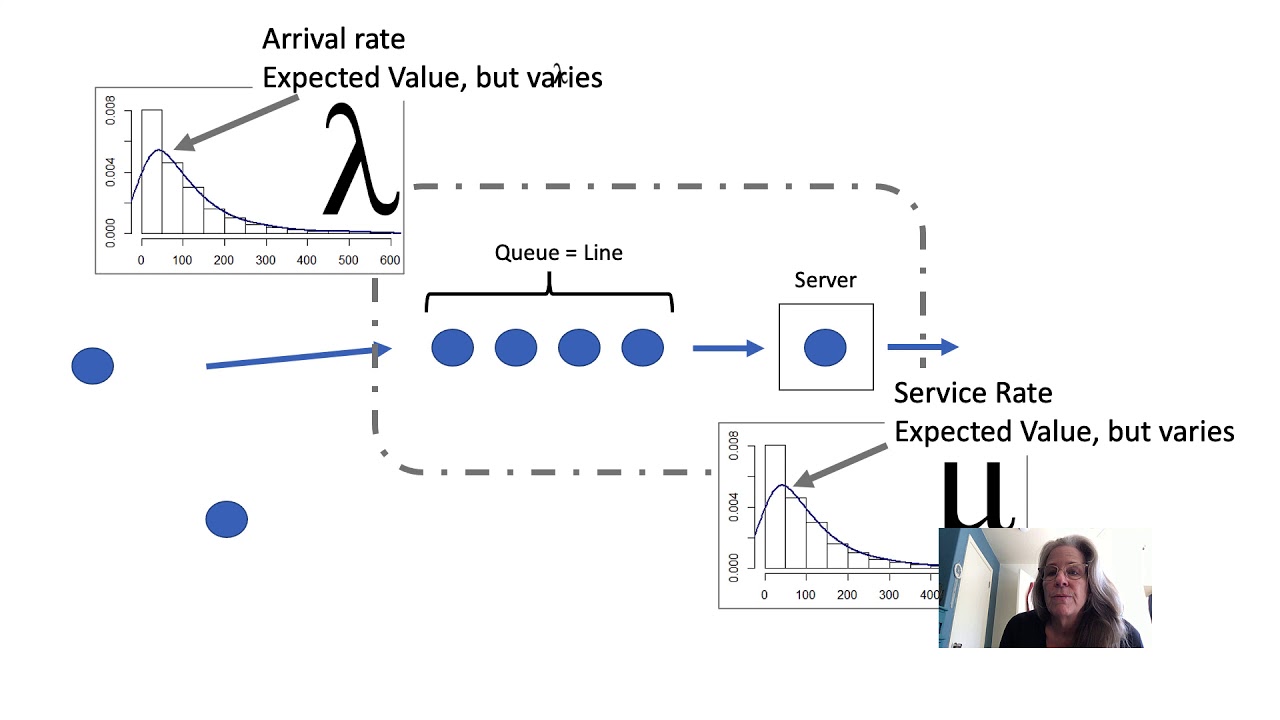
• 😀 TVs arrive at a rate of 20 per hour, and they undergo an adjustment process followed by an inspection.
• 😀 20% of inspected TVs fail and are rerouted back to adjustment, creating reentrant flow in the system.
• 😀 Selection weights are used to probabilistically route entities, with 20% of TVs failing inspection and re-entering the system.
• 😀 A tandem queuing model is used for system verification, where the adjustment and inspection stations are modeled as separate servers.
• 😀 The effective arrival rate at the adjustment station increases due to the reentrant flow from failing TVs.
• 😀 A reentrant flow model is developed using the equation Lambda' = Lambda / (1 - P), where P is the failure probability.
• 😀 The model is initially built with exponential distributions for processing times to facilitate comparison with the static queuing model.
• 😀 The simulation results are verified by comparing metrics such as utilization, time in the system, and number in the system with the static model.
• 😀 Reference properties in Simio are used to compare different scenarios, such as changing the processing time distribution from exponential to uniform.

Q & A

What is the main focus of the video in terms of system design?

The main focus is to design and verify a queuing model for a TV adjustment and inspection facility, where TVs fail inspection and must return for readjustment. The model incorporates reentrant flow and uses selection weights for routing entities through the system.

What is reentrant flow, and how does it impact the system?

Reentrant flow occurs when entities, after completing one part of the process (inspection in this case), fail and must return to a prior stage (adjustment). This increases the effective arrival rate to the adjustment station, as the flow includes both new and failed entities.

How is the effective arrival rate for the adjustment station calculated?

The effective arrival rate for the adjustment station is calculated using the formula Lambda Prime = Lambda / (1 - P), where Lambda is the nominal arrival rate and P is the probability of failure during inspection.

What are selection weights, and how are they used in Simio?

Selection weights are used in Simio to probabilistically route entities through different paths based on assigned weights. The probability of an entity following a path is the weight of that path divided by the sum of all weights, enabling controlled routing based on failure probabilities.

What happens if the sum of the selection weights does not equal one in Simio?

If the sum of the selection weights does not equal one, Simio will still correctly compute the probability for each path by dividing each path's weight by the total sum of all weights. The weights do not need to sum to one, as Simio calculates probabilities from the ratio of individual weights.

What distribution was initially used for processing times in the model, and why?

Initially, exponential distributions were used for the processing times in the model (both adjustment and inspection) to facilitate comparison with the static queuing model for verification purposes.

How does the change in processing time distribution affect the system's performance?

Changing the processing time distribution from exponential to uniform reduced both the time entities spent in the system and the number of entities in the system. This change was due to the reduced variance in processing times, which led to more predictable and efficient operation.

What is the purpose of verification in simulation modeling?

Verification ensures that the simulation model behaves as expected and produces results that are consistent with theoretical or real-world expectations. In this video, verification was conducted by comparing the simulation results with those from a static queuing model.

How is a reference property used in Simio to compare different model scenarios?

A reference property in Simio allows users to compare different scenarios by linking a property (such as processing time) to a control variable. By changing this property and running different scenarios, users can directly observe and compare the effects on performance metrics like time in system and number in system.

What is the significance of running multiple replications during the verification process?

Running multiple replications helps tighten the confidence intervals around performance metrics, making the results more reliable and ensuring that the model is accurately reflecting real-world behavior. In this case, increasing the number of replications improved the precision of the results.