118. Integración por partes, x por coseno (Algebraica por trigonométrica) (Ejemplo resuelto)
Summary
TLDREn este video de Mate Fácil, se resuelve una integral de x * coseno de x usando el método de integración por partes. Se explica cómo elegir la función u y db siguiendo la regla LIATE, y se detalla el proceso paso a paso. El resultado final es x * seno de x + coseno de x + C. El video invita a los espectadores a intentar resolver la integral de x * e^x antes del próximo video y los anima a dejar preguntas o sugerencias en los comentarios. Además, se pide apoyo a través de 'likes' y compartir el contenido.
Takeaways
- 📘 El video enseña cómo calcular la integral de x * coseno(x) * dx utilizando el método de integración por partes.
- 🔑 Se utiliza la fórmula de integración por partes: ∫u dv = uv - ∫v du para resolver la integral.
- 📚 Se elige 'x' como la función 'u' y 'coseno(x)' como 'dv' siguiendo la regla de LIATE (Logaritmos, Inversas, Algebraicas, Trigonometricas, Exponenciales).
- 🧮 La derivada de 'u' (x) es 1, por lo que 'du' es dx.
- 📐 La integral de 'dv' (coseno(x)) es 'seno(x)', lo que se convierte en 'v'.
- ✅ Se aplica la fórmula de integración por partes y se obtiene x * seno(x) - ∫seno(x) dx.
- 🔄 Se calcula la integral de 'seno(x)', que es -coseno(x), y se sustituye en la fórmula.
- 📉 El resultado final de la integral es x * seno(x) + coseno(x) + C, donde C es la constante de integración.
- 🎥 Se invita a los espectadores a intentar resolver el próximo desafío de integrar x * e^x * dx antes de ver el siguiente video.
- 👍 Se anima a los espectadores a dar like, compartir y comentar sus dudas o sugerencias en el canal.
Q & A
¿Cuál es la fórmula utilizada para resolver la integral por partes?
-La fórmula utilizada es: la integral de u * dv es igual a u * v menos la integral de v * du.
¿Qué es lo primero que se debe hacer al aplicar la regla de integración por partes?
-Lo primero es elegir las funciones u y dv de la integral original. En este caso, hay que seleccionar cuál función será u y cuál dv.
¿Qué regla se utiliza para seleccionar la función u en la integración por partes?
-Se utiliza la regla LIATE, que indica el orden en que se deben elegir las funciones para u: Logarítmica, Inversa, Algebraica, Trigonométrica y Exponencial.
¿Qué función se selecciona como u en este caso y por qué?
-Se selecciona la función algebraica, que es x, porque según la regla LIATE, las funciones algebraicas tienen prioridad sobre las trigonométricas.
¿Qué función se selecciona como dv y por qué?
-La función dv es lo que sobra de la integral original, que en este caso es coseno de X * dx.
¿Cómo se obtiene du a partir de u?
-du se obtiene derivando u, es decir, la derivada de x es 1, por lo que du es 1 * dx.
¿Cómo se obtiene v a partir de dv?
-v se obtiene integrando dv. La integral de coseno de X es seno de X.
¿Cuál es el resultado intermedio antes de resolver la segunda integral?
-El resultado intermedio es: x * seno de X menos la integral de seno de X * dx.
¿Cuál es el resultado de la integral de seno de X?
-La integral de seno de X es -coseno de X.
¿Cuál es el resultado final de la integral?
-El resultado final es: x * seno de X + coseno de X + la constante de integración.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Integración por partes ejemplo 2 | Cálculo integral - Vitual

Técnicas de integración | Integración por partes
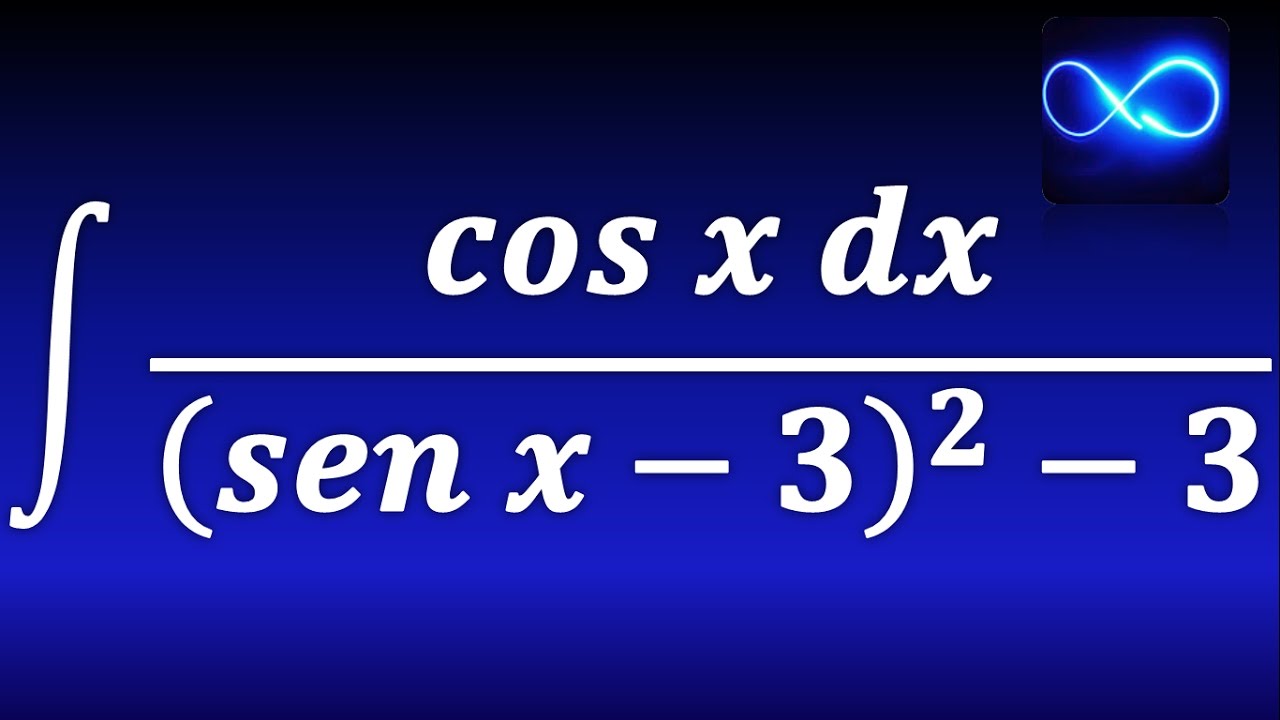
Integral de coseno entre seno cuadrado menos 3

INTEGRACIÓN por PARTES | Integrales Cíclicas

50. Integral indefinida por el método de Sustitución (Cambio Variable). Expresión con raíz cuadrada.

08. Límite con indeterminación 0/0
5.0 / 5 (0 votes)
