Non-Euclidean Geometry [Topics in the History of Mathematics]
Summary
TLDRThis script explores the foundations of geometry, questioning the validity of Euclidean geometry and the possibility of alternative geometries. It delves into the work of mathematicians like Gauss, Lobachevsky, and Riemann, who challenged traditional assumptions and developed non-Euclidean geometries, ultimately shifting the understanding of space and geometry from absolute truths to experimentally determined realities.
Takeaways
- 📚 Geometry is the study of space and has historically been considered a secure mathematical subject, but the foundations of Euclidean geometry were questioned in the 18th and 19th centuries.
- 🤔 The 'truth' of geometry, specifically whether Euclidean geometry accurately describes the space we live in, was doubted by mathematicians like Gauss, who believed it could not be proved.
- 🧐 Euclid's 5 postulates are the basis of his geometry, but the fifth postulate, the parallel postulate, was found to be less obvious and more contentious than the others.
- 📏 Attempts to prove the parallel postulate using the other postulates failed, leading to the exploration of alternative geometries.
- 🌐 Spherical geometry, which does not rely on the parallel postulate, was known in the 18th century and provides an example of an alternative to Euclidean geometry.
- 🔍 Geronimo Saccheri explored the possibility of non-Euclidean geometries by considering alternatives to the fifth postulate, leading to the discovery of two potential new geometries.
- 🌀 Janos Bolyai and Nikolai Lobachevsky independently developed non-Euclidean geometry, which assumes the existence of multiple lines through a point that do not meet a given line, contrary to Euclidean geometry.
- 📐 The development of non-Euclidean geometry led to the realization that geometry could be based on different sets of postulates and that Euclidean geometry was not the only logically consistent system.
- 📊 The use of functions in geometry, such as the angle of parallelism as a function of distance, was an innovative approach to understanding the properties of non-Euclidean spaces.
- 🌍 Bernhard Riemann expanded the concept of geometry to include any surface, not just flat ones, and proposed that geometry could be defined by intrinsic properties of the surface, such as curvature.
- 🌐 Eugenio Beltrami constructed a map of a surface with constant negative curvature, providing a model for non-Euclidean geometry and demonstrating its logical possibility.
Q & A
What was the main concern of mathematicians in the 18th and 19th centuries regarding the foundations of geometry?
-The main concern was whether Euclidean geometry was necessarily true and whether alternative geometries could exist, thus questioning the nature of space itself.
What was the 'truth of geometry' that Gauss was interested in?
-Gauss was interested in whether Euclidean geometry correctly describes the space we live in and if its truth could be proven or if it was just an assumption.
What is the significance of Euclid's fifth postulate, also known as the parallel postulate?
-The parallel postulate was significant because it was not as obviously true as the other postulates and its necessity for proving certain geometric theorems led to doubts about its validity.
Why did mathematicians attempt to prove the parallel postulate using the other four postulates of Euclid?
-They wanted to prove the parallel postulate to ensure that Euclidean geometry was based on self-evident truths and to eliminate the need for an unproven assumption.
What was the contribution of Geronimo Saccheri to the understanding of alternative geometries?
-Saccheri pioneered the idea of considering a geometry different from Euclid's by exploring the implications of alternative fifth postulates, leading to the discovery of non-Euclidean geometries.
What is spherical geometry and how does it relate to the concept of parallel lines?
-Spherical geometry is the geometry associated with the surface of a sphere, where 'straight' lines are great circles. It demonstrates that there can be no parallel lines, as any line must eventually meet another line on the sphere's surface.
What was the significance of Janos Bolyai and Nikolai Lobachevsky's work on non-Euclidean geometry?
-Bolyai and Lobachevsky independently developed non-Euclidean geometry, showing that it was logically consistent and thus challenging the notion that Euclidean geometry was the only possible description of physical space.
How did Bernhard Riemann contribute to the understanding of geometry?
-Riemann proposed that geometry could be done on any surface, introducing the idea of intrinsic properties of a surface to define its curvature and establishing that Euclidean geometry was just one of many possible geometries.
What is the significance of the angle sum of a triangle in non-Euclidean geometry?
-In non-Euclidean geometry, the angle sum of a triangle is not necessarily 180 degrees, which is a departure from the Euclidean model and an important characteristic of these alternative geometries.
How did Eugenio Beltrami's model of a non-Euclidean surface help in understanding negative curvature?
-Beltrami constructed a model that depicted a two-dimensional non-Euclidean space within a disc, showing that distances appear to shrink as one moves outwards, which is a characteristic of a surface with constant negative curvature.
What does the non-Euclidean model suggest about the nature of space?
-The non-Euclidean model suggests that space could be curved in ways other than what is described by Euclidean geometry, and that the true nature of space is a matter for empirical investigation rather than purely logical deduction.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Diferencias entre la Geometría Euclidiana y no Euclidiana
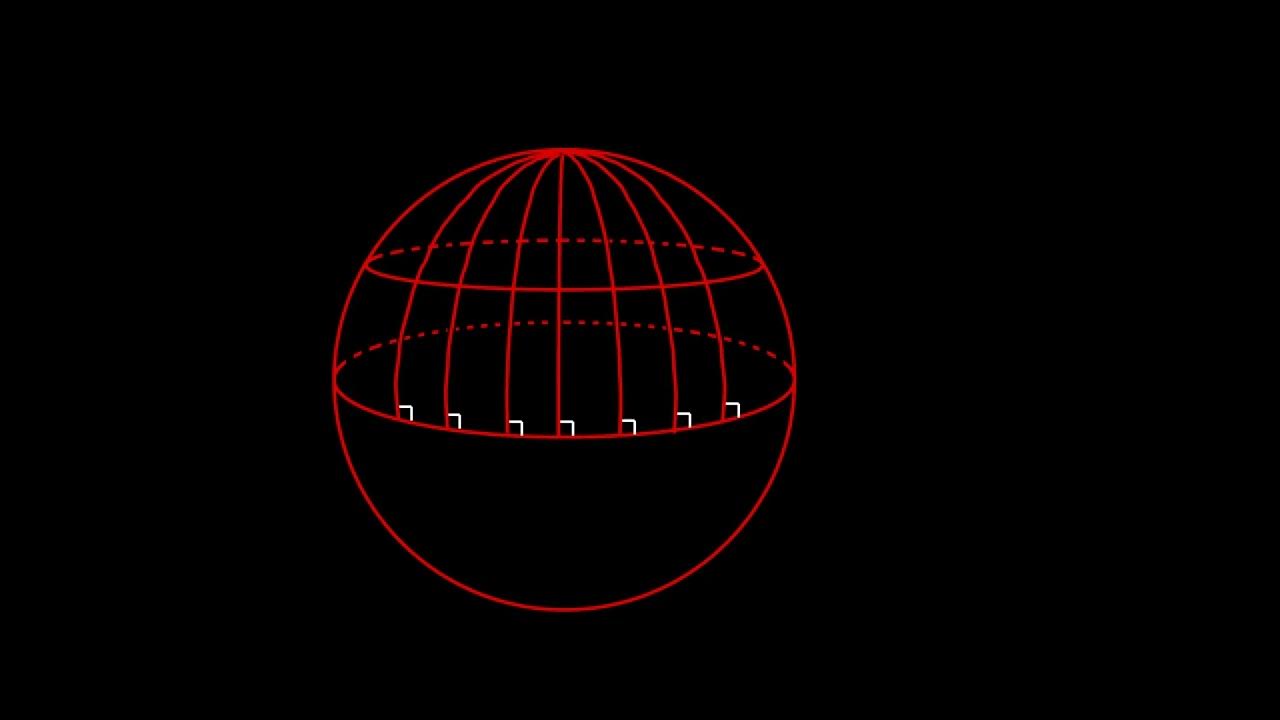
Classroom Aid - Non-Euclidean Geometry

Los Universos Paralelos Ocultos Vienen de Hace Muchos Años...
Electron Geometry vs Molecular Geometry: Explanation & Examples

A Problem with the Parallel Postulate - Numberphile

Greatest Math Theories Explained
5.0 / 5 (0 votes)