Diferencias entre la Geometría Euclidiana y no Euclidiana

Summary

This video explores the differences between Euclidean, Elliptic, and Hyperbolic geometries. It explains that Euclidean geometry operates on flat planes with zero curvature, where the sum of a triangle's interior angles is 180 degrees. In contrast, Elliptic geometry, with positive curvature (like a sphere), results in an angle sum greater than 180 degrees. Hyperbolic geometry, with negative curvature (like a saddle), causes the angle sum to be less than 180 degrees. These fundamental differences in curvature distinguish these three types of geometry and highlight their unique properties in the study of space.

Takeaways

• 😀 Euclidean geometry satisfies the five postulates of Euclid.
• 😀 In Euclidean geometry, the sum of the internal angles of a triangle is 180 degrees.
• 😀 Euclidean geometry has zero curvature, which means it is flat.
• 😀 Non-Euclidean geometry is divided into two main types: elliptical and hyperbolic geometry.
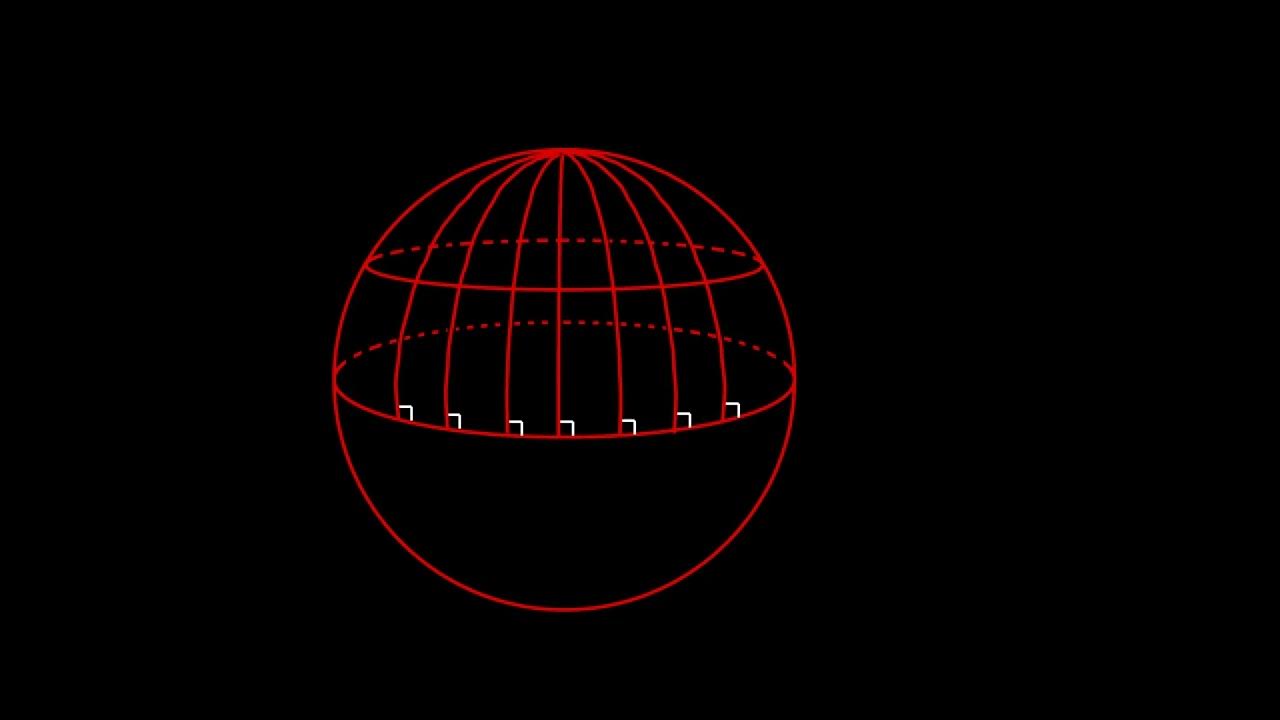
• 😀 Elliptical geometry has positive curvature.
• 😀 In elliptical geometry, the sum of the internal angles of a triangle is greater than 180 degrees.
• 😀 In hyperbolic geometry, the sum of the internal angles of a triangle is less than 180 degrees.
• 😀 Hyperbolic geometry has negative curvature, meaning it is curved in the opposite direction to Euclidean geometry.
• 😀 A real-world example of elliptical geometry can be seen in the surface of a sphere, where triangles have angles summing to more than 180 degrees.
• 😀 A real-world example of hyperbolic geometry can be seen in the surface of a saddle, where triangles have angles summing to less than 180 degrees.

Q & A

What is the key distinction between Euclidean geometry and non-Euclidean geometry?

Euclidean geometry satisfies the five postulates set by Euclid, while non-Euclidean geometry includes different types, such as elliptic and hyperbolic geometries, which do not follow all of Euclid's postulates.

What are the fundamental properties of Euclidean geometry?

Euclidean geometry is based on five postulates and is characterized by flat space, where the sum of the interior angles of a triangle equals 180 degrees, and the curvature of space is zero.

In Euclidean geometry, what is the sum of the interior angles of a triangle?

In Euclidean geometry, the sum of the interior angles of a triangle is always 180 degrees.

What does a curvature of zero mean in Euclidean geometry?

A curvature of zero means that the space is flat, and geometric properties such as the sum of angles in a triangle remain constant, like 180 degrees.

What is elliptic geometry and how does it differ from Euclidean geometry?

Elliptic geometry is a type of non-Euclidean geometry where the space has positive curvature. In this geometry, the sum of the interior angles of a triangle is greater than 180 degrees, contrasting with Euclidean geometry.

What happens to the sum of the angles in a triangle in elliptic geometry?

In elliptic geometry, the sum of the interior angles of a triangle is greater than 180 degrees due to the positive curvature of the space.

Can you provide an example of elliptic geometry?

An example of elliptic geometry is the surface of a sphere, where triangles are drawn on the surface and their interior angles exceed 180 degrees.

What is hyperbolic geometry and how does it differ from Euclidean geometry?

Hyperbolic geometry is another form of non-Euclidean geometry where space has negative curvature. In hyperbolic geometry, the sum of the interior angles of a triangle is less than 180 degrees.

What happens to the sum of the angles in a triangle in hyperbolic geometry?

In hyperbolic geometry, the sum of the interior angles of a triangle is less than 180 degrees due to the negative curvature of the space.

What is a real-world example of hyperbolic geometry?

A real-world example of hyperbolic geometry is the surface of a saddle, like the shape of a horse's saddle or a 'silla de montar' in Spanish, where geometric properties differ from those in flat space.