A Problem with the Parallel Postulate - Numberphile

Summary

This script delves into the parallel postulate of Euclidean geometry, originally from Euclid's Elements, and its implications in different geometrical models. It explains the postulate's traditional interpretation in plane geometry, where through a point not on a given line, there's exactly one non-intersecting line. The script then contrasts this with spherical geometry, where no parallel lines exist, and hyperbolic geometry, where multiple parallel lines are possible. The discussion highlights the postulate's uniqueness and the diversity of geometrical systems, challenging the idea that it's a necessary consequence of Euclid's first four postulates.

Takeaways

• 📚 The parallel postulate is a fundamental concept in Euclidean geometry, first introduced in Euclid's Elements around 300 BC.
• 🔍 The postulate states that for a given line and a point not on the line, there is exactly one line through the point that does not intersect the original line, emphasizing uniqueness.
• 🤔 The parallel postulate was historically considered a prime example of deductive reasoning, where truths are derived from a set of axioms.
• 🌐 The script discusses the limitations of the parallel postulate by introducing non-Euclidean geometries, such as spherical geometry, where the postulate does not hold.
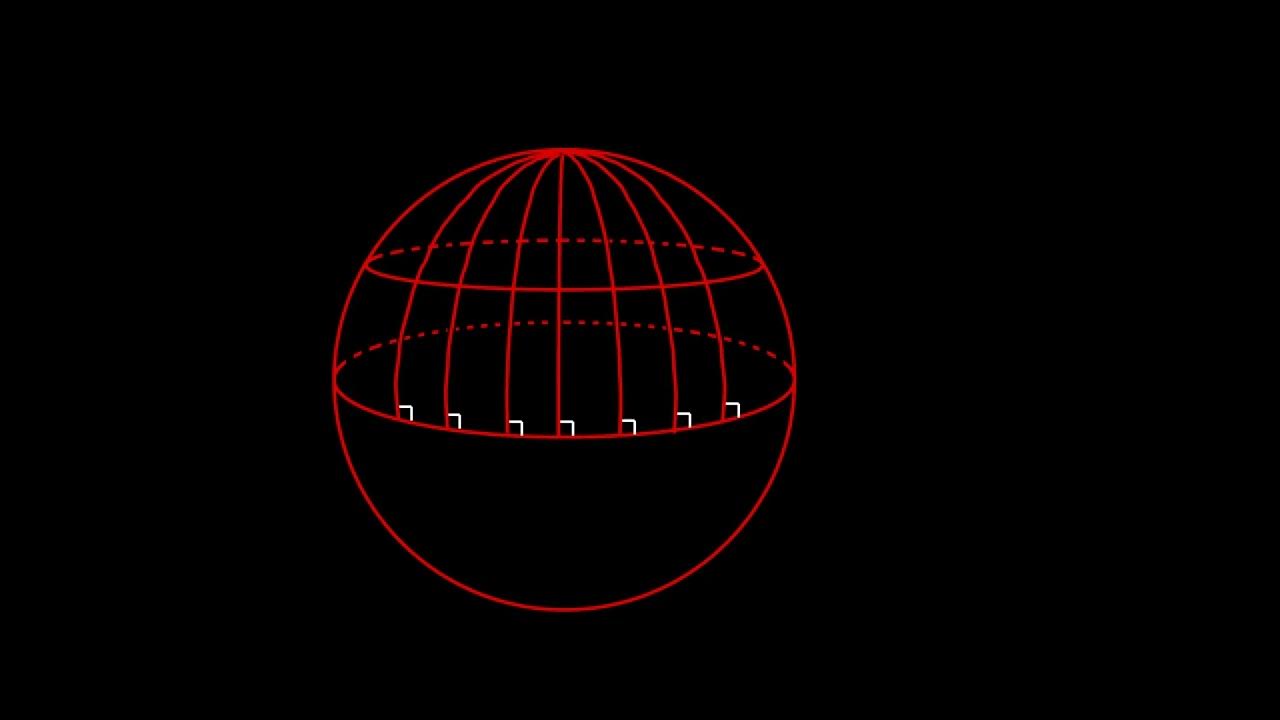
• 🌍 In spherical geometry, represented by a 2D surface on a sphere, there are no parallel lines because any line (great circle) through a point not on a given line will intersect it.
• 📏 The concept of a 'line' in spherical geometry differs from the Euclidean plane, with 'lines' being great circles or segments of great circles.
• 🛑 The failure of the parallel postulate in spherical geometry indicates that it is not a necessary consequence of the first four postulates of Euclid.
• 🔄 The script also introduces hyperbolic geometry, another non-Euclidean geometry where there are infinitely many parallel lines to a given line through a point not on it.
• 📊 In hyperbolic geometry, lines are defined differently, either as straight lines through the center of the model or as segments of circles orthogonal to the boundary.
• 🧩 The existence of non-Euclidean geometries shows that there are multiple ways to approach two-dimensional geometry, challenging the uniqueness of the Euclidean model.
• 💭 The script suggests that Euclid might have been aware of the peculiar nature of the parallel postulate, as it was not used in his work until later sections.

Q & A

What is the parallel postulate?

The parallel postulate is a statement in Euclidean geometry that asserts that through a point not on a given line, there is exactly one line parallel to the given line. It was originally presented by Euclid in his 'Elements' around 300 BC.

Why was the parallel postulate significant in the 19th century?

In the 19th century, the parallel postulate was considered an example of what it means to know something. It was highly valued because it represented the deductive nature of geometry, where truths are derived from a set of axioms.

What is the difference between a line and a line segment in the context of the parallel postulate?

In the context of the parallel postulate, a line is an infinite straight path that extends indefinitely in both directions, while a line segment is a part of a line that is bounded by two distinct end points and has a finite length.

How is the parallel postulate stated in Euclid's 'Elements'?

In Euclid's 'Elements', the parallel postulate is stated in terms of angles. If a line and a point not on the line create two angles that sum to less than 180 degrees, the lines, when extended to infinity, will intersect.

What is a model of geometry where the parallel postulate does not hold?

A model of geometry where the parallel postulate does not hold is spherical geometry, where the surface is a sphere, and lines are represented by great circles, such as the equator or lines of longitude.

What is a great circle in spherical geometry?

A great circle in spherical geometry is the largest circle that can be drawn on the surface of a sphere. It is the intersection of the sphere with a plane that passes through the center of the sphere.

How does the concept of distance differ between Euclidean and spherical geometry?

In Euclidean geometry, distance is measured using a straight line between two points, following the Pythagorean theorem. In spherical geometry, distance is measured along the shortest path on the sphere's surface, which is along a great circle.

What is hyperbolic geometry and how does it relate to the parallel postulate?

Hyperbolic geometry is a non-Euclidean geometry where the parallel postulate is replaced by the existence of more than one line through a point parallel to a given line. In this geometry, lines are represented by segments of circles orthogonal to the boundary of a disk.

Why was there an upheaval in geometry in the 19th century regarding the parallel postulate?

The upheaval in geometry in the 19th century occurred because mathematicians discovered that the first four postulates of Euclid could be used in other geometries, such as spherical and hyperbolic geometry, without the fifth postulate, showing that it was not a necessary consequence of the others.

What does the failure of the parallel postulate in spherical and hyperbolic geometries imply about the nature of geometry?

The failure of the parallel postulate in spherical and hyperbolic geometries implies that there are multiple consistent ways to do geometry in two dimensions, each with its own set of rules and properties, challenging the idea of a single, universal geometry.

How did the understanding of the parallel postulate evolve over time?

Initially, the parallel postulate was accepted as a fundamental truth in Euclidean geometry. However, with the development of non-Euclidean geometries in the 19th century, it became clear that the postulate was not universally true and was instead a specific case within a broader spectrum of geometric possibilities.

Outlines

00:00

📚 Introduction to the Parallel Postulate

The first paragraph introduces the parallel postulate, a fundamental concept in Euclidean geometry that has been historically considered a cornerstone of knowledge and deductive reasoning. The postulate, which was first presented in Euclid's Elements around 300 BC, states that for a given line and a point not on the line, there exists exactly one line through the point that does not intersect the original line. This principle is a key element taught in high school geometry and is often taken for granted as an obvious truth. The paragraph also touches on the historical significance of the postulate and its presentation in Euclid's work, highlighting the difference between the original phrasing and the common understanding of the concept.

05:03

🌐 Exploring the Parallel Postulate in Spherical Geometry

The second paragraph delves into the application of the parallel postulate in spherical geometry, contrasting it with the Euclidean plane. It explains that in a spherical model, such as the surface of a sphere, the concept of a line is represented by a Great Circle, the intersection of a sphere with a plane passing through its center. The paragraph discusses the process of defining lines and points in spherical geometry and challenges the parallel postulate by illustrating that in this non-Euclidean space, there are no lines that are parallel to a given line through a point. This revelation shows that the postulate does not hold universally and depends on the geometric model being considered.

10:06

🔍 Hyperbolic Geometry and the Abundance of Parallels

The third paragraph explores hyperbolic geometry, another non-Euclidean geometry where the parallel postulate is significantly altered. In this model, represented by a disk with lines being either straight lines through the center or circular segments orthogonal to the boundary, there are infinitely many lines that can be drawn through a point that do not intersect a given line. This stands in stark contrast to the Euclidean postulate, which asserts the uniqueness of such a line. The paragraph discusses the implications of this for the understanding of the parallel postulate and how it highlights the diversity of geometric systems that can exist beyond the traditional Euclidean framework.

Keywords

💡Parallel Postulate

The Parallel Postulate is a fundamental concept in Euclidean geometry, stating that through a point not on a given line, there is exactly one line parallel to the given line. In the video, it is discussed as the fifth postulate of Euclid's Elements, which historically has been a cornerstone of deductive reasoning in geometry. The script explores its uniqueness and challenges in different geometric contexts, such as spherical and hyperbolic geometry.

💡Euclid's Elements

Euclid's Elements is a classical work in mathematics, compiled by the ancient Greek mathematician Euclid in 300 BC. It laid the foundation for much of the Western mathematical tradition, especially in geometry. The video script references this work as the origin of the parallel postulate and discusses its historical significance and influence on the understanding of geometry.

💡Deductive Reasoning

Deductive reasoning is a method of logic where conclusions are reached based on the acceptance of certain premises or rules. In the context of the video, deductive reasoning is highlighted as the method by which Euclidean geometry operates, using a set of axioms to derive theorems, with the parallel postulate being one of those foundational rules.

💡Spherical Geometry

Spherical Geometry is a type of non-Euclidean geometry that takes place on the surface of a sphere. The video script introduces spherical geometry as an alternative model to the Euclidean plane and discusses how the parallel postulate does not hold in this space, as there are no parallel lines that do not intersect on a sphere.

💡Great Circle

A Great Circle is a circle on the surface of a sphere whose center coincides with the center of the sphere. In the video, the concept of a great circle is introduced as the equivalent of a 'line' in spherical geometry, which is used to explore the failure of the parallel postulate in this context.

💡Hyperbolic Geometry

Hyperbolic Geometry is another form of non-Euclidean geometry, characterized by the existence of more than one parallel line through a given point not on a given line. The script contrasts hyperbolic geometry with Euclidean geometry by showing that the parallel postulate is violated in this system, as there are infinitely many parallels to a given line through a point outside it.

💡Euclidean Geometry

Euclidean Geometry is the geometry of flat, two-dimensional spaces, based on the axioms and postulates set forth by Euclid. The video script uses Euclidean geometry as a reference point for the discussion of the parallel postulate and its implications in other geometric systems.

💡Meridians and Latitude

Meridians and latitude are terms used to describe positions on the Earth's surface, with meridians being lines running from the North Pole to the South Pole and latitude being the angle between a point on the Earth and the equator. In the video, these terms are used to explain the concept of coordinates in spherical geometry.

💡Pythagorean Theorem

The Pythagorean Theorem is a fundamental principle in Euclidean geometry that states the relationship between the sides of a right-angled triangle. In the script, it is mentioned as the basis for measuring distances in a plane, which is a concept that is revisited when discussing different geometric models.

💡Non-Euclidean Geometries

Non-Euclidean Geometries are geometries that do not subscribe to the parallel postulate of Euclidean geometry. The video script delves into spherical and hyperbolic geometries as examples of non-Euclidean systems, showing that they offer alternative ways of understanding space and challenging the traditional axioms of Euclidean geometry.

💡Geometric Models

Geometric Models refer to different conceptualizations of space and the rules governing it. The video script discusses various geometric models, such as the Euclidean plane, the sphere (spherical geometry), and the disk (hyperbolic geometry), to illustrate how the parallel postulate's validity varies across these models.

Highlights

Introduction to the parallel postulate and its origin in Euclid's Elements.

The parallel postulate as a foundational principle in deductive reasoning within geometry.

Explanation of the parallel postulate in high school geometry terms.

The uniqueness of the parallel line through a point not on a given line.

Euclid's original phrasing of the parallel postulate involving angle sums.

The parallel postulate's validity depending on the model of geometry considered.

Introduction of spherical geometry as an alternative to Euclidean geometry.

Description of a sphere (S2) as a 2-dimensional space for geometry.

The concept of meridians and latitudes as coordinates in spherical geometry.

The absence of parallel lines in spherical geometry, contradicting the parallel postulate.

Historical context of spherical geometry in navigation and astronomy.

Definition of a 'line' in spherical geometry as a Great Circle.

The distinction between a line segment and a line in the context of spherical geometry.

Introduction to hyperbolic geometry as another model where the parallel postulate does not hold.

Description of lines in hyperbolic geometry as either straight lines through the center or circle segments orthogonal to the boundary.

The existence of infinitely many parallel lines in hyperbolic geometry, contrasting with Euclidean geometry.

The parallel postulate's role in the development of non-Euclidean geometries.

Discussion on the philosophical and historical significance of the parallel postulate in geometry.

Euclid's delayed use of the parallel postulate in his Elements as a potential clue to his unease with it.

The appreciation of the parallel postulate for enabling the understanding of multiple geometries.

Transcripts

Today I am going to tell you about the  parallel postulate in geometry. Well let  

me start by telling you what it is, right? So this  originally appears in Euclid's Elements - it's, I  

think, published 300 BC. It's what we inherited  as geometry, right, and it was in fact for a very  

long time, especially in the 19th century, taken to  be the example of what it means to know something,  

right. We like it because it's deductive - you  know, you have a set of rules, and then from  

those rules you derive some truths. So what is  the parallel postulate? And this is something  

that we actually learn in high school geometry.  If we are given a line in our plane now, here we  

have a point P, a point that is not in the line. Then  what we can do is we can we can draw many lines  

that go through that point P but what Euclid told  us, and that was the parallel postulate, is that  

there's a unique line that does not intersect L  and goes through the point P. - (Brady: One and only one.)

One and only one. That is that is the key here, one  and only one. There exists one and it is unique.  

And that's what we took to be true. - (That seems to me like the most obvious thing in the world.)

(Because if I draw any other line it's  got that slight angle which means it's going)  

(to be- one side of it is going to be tipping towards L.) - Right right right. And in fact, you know, like- 

so this is a little bit of a lie because if you  open Euclid's Element you're not going to find  

this statement the way it is written. So in fact  the way he wrote it is more similar to what you  

were saying; what he said is, you know, if you have  a line and then you have the point P you draw your  

line through P then - let me draw just any other  line through P to help. What he said is if  

the sum of these two angles is less than 180  degrees then the lines, once you extend them to  

infinity, they're going to intersect. - (Right, classic Euclid, parallel postulate- seems true to me.) - Yes exactly  

exactly and it- well in fact it seems true to you  and to most of us because it is actually true. But  

it sort of depends on the model of geometry that  we're considering, right? So here we're working on  

a plane and to do geometry we need among many  other things a way of measuring distance. And, you  

know, like if we're here in the plane we measure  distances with a ruler. Or if you want, you know,  

like there's a formula if you have coordinates - um it's basically the Pythagorean theorem. So we have-

we know what we're doing; however that is not  the only space in which we can do geometry. 

Not even 2-dimensional space, right, so the plane  we have a vertical direction and a horizontal  

direction, those are our two dimensions right? Let  me show you another space where we can do geometry.

Here's what we call a sphere, so as mathematicians  call it S2. If you're a mathematician then you  

draw R3, 3-dimensional space, and you say  that this is the set of points that are at  

distance 1 from the origin. If you're not a  mathematician you're just looking at the shell  

of a football ball. - (Is this a 2-dimensional space or?) - This is a 2-dimensional space because  

again we basically only have two directions  in which to move right. So if you want we can  

do it in terms of meridians and latitude, right,  the way we do it to describe location, right. Like  

if you look in Google Maps, if you want a precise  location, you're going to get two coordinates.  

Exactly that. - (Okay so although although we think  of balls and things as 3-dimensional objects,)  

(because we're only dealing with the shell it's  a 2-dimension?) - Exactly yeah and that is very  

important, we're not thinking about the filling. We're- you know, we're thinking about a  

little ant that is just completely flat. - (So what happens to the parallel postulate here?) - Well so,  

you know, here I started by telling you there's a  line and there's a point, right? So I have to tell you the same thing here.

I have to define my objects. So a line in here is  going to be what we call a Great Circle. What is a  

great circle? Take the intersection of this sphere  with a plane that that goes through the origin - so  

this is a great circle. Or, you know, the way I drew  it here this is the equator, that's also going to  

be a great circle. - (So every line has to like- through the longest possible line does it? It can't be)  

(just a little circle?) - Aha! So that's- so this is key  right? So there's a difference between what we call  

a line and what we call a line segment, right. And  actually so that line segments, that's one of the  

first rules that we have in Euclidean geometry or  in in the geometry of the plane; which is that if  

I give you two points you're going to be able  to give me a line. In our plane geometry that's  

pretty easy, two points, we get a ruler, here's the  line right. Pretty easy, we know how to do it. Here it's a  

little trickier but is is not so bad. If you choose  a point say over here, and then maybe a point over  

here, then how do I find the great circle that  goes through them, right? And and I need to find  

the great circle and then only look at that little  segment that connects them. And that's another- that  

little segment. Well, we can do it um by choosing- you know, like we can extend these points, join  

them to the origin. There's a little space in  between them, let me fill that with a plane. 

That's the plane that's going to intersect my  sphere, it's going to be something like that.  

(So you're trying to find the equator basically that-  on which both of those lines sit?) - Exactly, exactly,

except you know like it's a tilted equator right?  Like it's not- but yes that is basically it. I could  

have- I mean I could have cheated and just chosen  two points in in the equator but. But so what I  

drew here is a line, right, so the line segment. Well,  we have two options: this very clearly short one; 

but then there's another one that is longer and  it goes around. Sometimes what we say is that a  

line segment is the segment that- whose length is  less than half of the entire circumference. That  

fixes some issues. - (So what does this mean for the parallel postulate?) - Excellent question. So let me do-  

let me draw my sphere here again. I'm going to draw  a line that is easier for me, again this meridian.  

That's my line, so this is my line L, and then I'm  going to get my point P. Let me choose this  

point P right. So lines that go through P: there's  this one, so here we have a problem, right we have  

this intersection and this intersection. So maybe  we need another one right? Okay so maybe maybe  

we draw the line segment, or the whole line, that  goes through P and then another point over here.  

Okay, we draw it. - (No good.) - No good. So turns out that what happens in the 2-sphere is that there  

are no parallel lines. So before we said that in  the plane there existed one and it was unique,  

so here we don't even have that first part of  existence - we're done. - (Okay. But I mean that's) 

(not- that's not Euclid's fault. He wasn't talking about-) - No, no no no no no no no absolutely not. It's  

actually kind of interesting because there was  a lot of research being done in in the geometry  

of the sphere, or trigonometry maybe to be more  precise, because people needed this for navigation  

and for astronomy - or astrology for some people  too. You know, like everything that had to do with  

the skies was a sphere. So there was a lot of  knowledge but somehow nobody thought that we  

could think about these two spaces as similar, as  both sharing a set of rules, right. It wasn't until  

maybe later that we- in the 19th century that there  was an upheaval in geometry when we realized that  

in fact if you consider the first four postulates  of Euclid, there are older models where you can do  

geometry that holds- you know, that has those four  rules except for that fifth one. - (So that- so his)  

(first four rules hold up in other spaces? But this  is the one that doesn't transfer across?) - Yeah. It-  

may- you know maybe to be precise uh it might be a  modern restatement of his axioms or postulates.  

Right, like we we had to get rigorous. The one  model, or the one geometry, that people started to  

think about to show that the parallel postulate  was just not true in general was not spherical  

geometry but hyperbolic geometry. This is going to  be a disk, let me draw the center. And again I have  

to tell you what it means to have a line. So a line,  it's either going to be a straight line that goes  

through the center or if I move a little bit away  from the center it's going to be the segment of a  

circle that is orthogonal to the boundary circle  of the disk. So are there parallel lines, right?  

Well in this case we are going to have parallel  lines but we're going to have too many. So that's  

sort of like the other problem right? Like we said:  there exists, and is unique. We already saw a place  

where they do not exist, now we have one where they  do exist but they're not unique. So what happens  

here is um- so let me say again that this is my  line L, why not, and let's say this is my point P.  

Well that's one line that goes through P, doesn't  intersect L, great, but I can draw more. I can sort of  

move my circles. I could just do many many more  because in fact they're going to be infinitely  

many. So the length here; again, you know, going back  to this distinction between a line segment and a  

line - this circle is a line. It sort of looks like  it's like finite, right? Like here a line is like  

the one that extends forever. The way we measure  distances here is such that if you have two points  

that are very close to the border, these two points  are very very very far away from each other. Even  

though you know like we're looking at it, and if we  were using the distance measurement that we had in  

in the plane, they look very close to one another;  but the way we measure things in this new geometry  

makes them be very far away. - (This postulate has failed us again) - Yes exactly, except you know it  

failed us um in the sense that it- it doesn't hold  right, so that immediately means that it- it is not  

a consequence of the first four rules which was  actually a question that people had for a very  

long time. Could it be derived from the first four  postulates? And now we see that's just not the case. 

(Clearly this fifth one was a bit of an add-on, it's not part of the family.) - It's not a part of the  

family no, no not exactly. And in fact- - (Can the- can the other four be derived from each other?) - No, no no  

no no those are sort of- you know, like the the four  of them are the minimal set of rules that you need  

um to play the game of geometry if you want.  Yeah but, you know, like in fact in in Euclid's  

Elements, if you analyze it you know like maybe in  a philosophical or historian of science way, you  

realize that Euclid waits a while before using the  parallel postulate, right? He uses the first four  

back and forth, back and forth, but the the  fifth one he waits a little bit. - (That was a clue.)  

That's what some people think, yeah, so maybe  he was uneasy about it a little bit.

(Does the- does this make you feel more affectionately  towards the fifth one or less affectionate towards)  

(it? Do you think of it as an ugly aberration  or does it make you feel it's more charming?)

I think it's- well I don't know if charming  but you know like it's a lot more important,

right, because it just allows us to think of  more than one way of doing geometry in two  

dimensions. That's- that's just fascinating.   

...the angle is less than two right angles.

(It's not catchy is it?) No, there's a lot of words, it's wordy. And  

let's let's see what it means. Two straight lines  for instance, we're going to put a third one in...