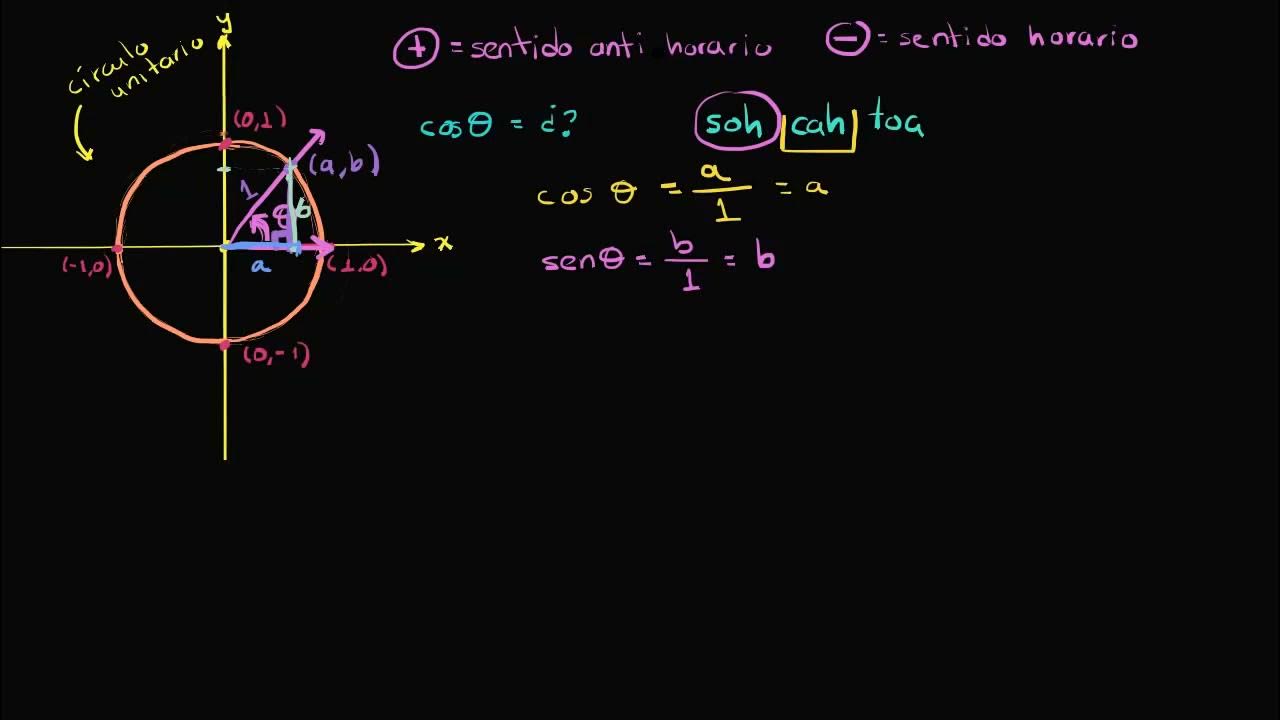CIRCUNFERÊNCIA TRIGONOMÉTRICA (AULA 2/24)

Summary

In this video, Professor Paulo Pereira provides an in-depth introduction to the unit circle in trigonometry. He explains the concept of the unit circle, positioned on the Cartesian plane, with a radius of one, and how its angular measures in radians are directly related to arc lengths. The video explores the division of the circle into four quadrants, detailing the positive and negative direction of angular movement. Additionally, the lesson covers key angular measures such as 0°, 90°, 180°, and 270° (or 0, π/2, π, 3π/2 radians), and the intervals for each quadrant. The professor also highlights the importance of understanding these foundational concepts for future exercises in trigonometry.

Takeaways

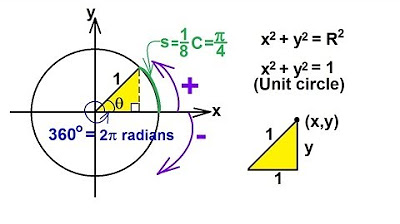
• 😀 The unit circle in trigonometry has a radius of 1 and is centered at the origin of the Cartesian plane.
• 😀 The circumference of the unit circle is numerically equal to the angular measure in radians due to its radius being 1.
• 😀 A full revolution around the unit circle corresponds to 360 degrees or 2π radians.
• 😀 The unit circle is divided into four quadrants: first, second, third, and fourth, with the positive direction being counterclockwise (anticlockwise).
• 😀 The angles in the unit circle are measured counterclockwise, with 0 radians (0°) being at the positive x-axis.
• 😀 Key angle measures in radians are: 0 radians (0°), π/2 radians (90°), π radians (180°), 3π/2 radians (270°), and 2π radians (360°).
• 😀 The angles 0°, 90°, 180°, and 270° are considered axis angles and do not belong to any quadrant specifically.
• 😀 Arcs in the first quadrant range from 0 to π/2 radians, in the second quadrant from π/2 to π radians, in the third quadrant from π to 3π/2 radians, and in the fourth quadrant from 3π/2 to 2π radians.
• 😀 Positive angles in the unit circle are measured counterclockwise, while negative angles are measured clockwise.
• 😀 Understanding the division of the unit circle into quadrants and the corresponding angle intervals is essential for solving trigonometric problems.

Q & A

What is the purpose of the trigonometric circle?

The trigonometric circle is a circle with a radius of one, positioned on the Cartesian plane. It is used to define angles and their corresponding trigonometric functions. The center of the circle coincides with the origin of the Cartesian plane.

Why is the radius of the trigonometric circle chosen to be one?

The radius is chosen to be one because it makes the numerical value of the length of any arc on the circle equal to its angular measurement in radians. This simplifies the relationship between linear and angular measurements and is advantageous for calculations.

How is the angular measurement of a full revolution represented?

A full revolution is 360° or 2π radians. The choice of radians as a unit of angular measurement aligns the length of the arc with the angular distance in a simple manner.

What are the key angle measurements on the unit circle?

The key angle measurements on the unit circle are 0° (0 radians), 90° (π/2 radians), 180° (π radians), 270° (3π/2 radians), and 360° (2π radians). These angles correspond to specific points on the circle's axes.

What is the significance of the direction in which the angles are measured on the unit circle?

Angles are measured counterclockwise from the positive x-axis, which is considered the positive direction. If the angle is measured clockwise, it is considered negative.

What is the difference between axis angles and quadrant angles?

Axis angles, such as 0°, 90°, 180°, and 270°, do not belong to any quadrant. They are simply the angles where the trigonometric circle intersects the axes. Quadrant angles, on the other hand, are angles that fall between these axis angles and lie within the four quadrants of the circle.

What does 'x belongs to the first quadrant' mean?

'x belongs to the first quadrant' means that the angle x is between 0 and π/2 radians (0° and 90°). It indicates that the angle lies in the first quadrant of the unit circle.

How is the second quadrant represented on the unit circle?

The second quadrant is represented by angles between π/2 and π radians (90° to 180°). Any angle in this range belongs to the second quadrant.

What is the notation for angles in the third quadrant?

Angles in the third quadrant are represented by the interval from π to 3π/2 radians (180° to 270°). Any angle in this range belongs to the third quadrant.

How is the fourth quadrant represented on the unit circle?

The fourth quadrant is represented by angles between 3π/2 and 2π radians (270° to 360°). Any angle in this range belongs to the fourth quadrant.