Círculo unitario. Definición de funciones trigonométricas

Summary

In this video, the concept of the unit circle is introduced to explain trigonometric functions. The circle is centered at the origin, with a radius of 1, and its coordinates help define the cosine and sine of angles. Positive angles move counterclockwise, and negative ones move clockwise. The video extends the classic SOH CAH TOA mnemonic to account for all angles using the unit circle, offering a more universal approach to understanding trigonometry. It also emphasizes how the unit circle helps define trigonometric functions for angles beyond 0° to 90°.

Takeaways

• 😀 The unit circle is centered at the origin (0,0) and has a radius of 1.
• 😀 The main coordinates of the unit circle are (1, 0), (0, 1), (-1, 0), and (0, -1).
• 😀 Positive angles are measured counterclockwise from the positive x-axis, while negative angles are measured clockwise.
• 😀 The angle θ is drawn from the positive x-axis, and the coordinates where the terminal side of the angle intersects the unit circle are (a, b).
• 😀 The cosine of an angle θ is equal to the x-coordinate of the point of intersection on the unit circle: cos(θ) = a.
• 😀 The sine of an angle θ is equal to the y-coordinate of the point of intersection on the unit circle: sin(θ) = b.
• 😀 The mnemonic SOH CAH TOA is useful for remembering trigonometric ratios for right triangles but doesn't extend to angles greater than 90° or negative angles.
• 😀 Using the unit circle allows us to define trigonometric functions for all angles, including those greater than 90° or negative angles.
• 😀 The cosine of an angle θ is the x-coordinate, and the sine of an angle θ is the y-coordinate of the point where the terminal side intersects the unit circle.
• 😀 The tangent of an angle θ is the ratio of sine to cosine: tan(θ) = sin(θ) / cos(θ).
• 😀 The unit circle provides a more generalized and robust way to define trigonometric functions that work for all angles, both positive and negative.

Q & A

What is a unit circle?

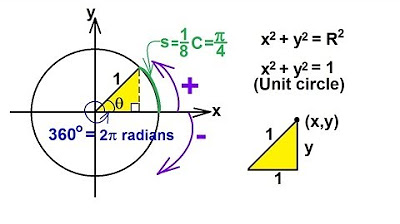
A unit circle is a circle centered at the origin (0, 0) with a radius of 1. This means any point on the circle has a distance of 1 from the center.

What are the coordinates of the four primary points on the unit circle?

The four primary points on the unit circle are: (1, 0) on the positive x-axis, (0, 1) on the positive y-axis, (-1, 0) on the negative x-axis, and (0, -1) on the negative y-axis.

What is the convention for positive angles on the unit circle?

Positive angles on the unit circle are measured counterclockwise from the positive x-axis, in an anti-clockwise direction.

How are negative angles defined on the unit circle?

Negative angles are measured in a clockwise direction, which is the same direction as the movement of the hands of a clock.

How does the unit circle help define trigonometric functions?

The unit circle allows us to extend trigonometric functions beyond acute angles. It defines the sine and cosine of any angle as the y and x coordinates, respectively, of the point where the terminal side of the angle intersects the circle.

What is the relationship between the sides of the right triangle formed in the unit circle?

In the right triangle formed by the unit circle, the hypotenuse is always 1 (the radius of the unit circle). The adjacent side is represented by the x-coordinate (cosine), and the opposite side is represented by the y-coordinate (sine).

What is the mnemonic SOH CAH TOA and how is it applied?

SOH CAH TOA is a mnemonic used for remembering trigonometric ratios: SOH (sine = opposite/hypotenuse), CAH (cosine = adjacent/hypotenuse), and TOA (tangent = opposite/adjacent). The unit circle provides an alternative definition for these functions, extending them beyond right triangles.

What happens when we attempt to apply SOH CAH TOA to angles greater than 90° or negative angles?

SOH CAH TOA is limited to angles between 0° and 90° since it relies on right triangles. For angles greater than 90° or negative angles, it becomes challenging to apply this mnemonic, which is where the unit circle provides a more comprehensive definition of the trigonometric functions.

How does the unit circle redefine the cosine and sine of any angle?

On the unit circle, the cosine of an angle θ is defined as the x-coordinate of the point where the terminal side of the angle intersects the circle. Similarly, the sine of the angle θ is the y-coordinate of the same point.

What is the definition of tangent using the unit circle?

The tangent of an angle θ, according to the unit circle, is defined as the ratio of sine to cosine (y/x), which corresponds to the ratio of the y-coordinate to the x-coordinate of the point of intersection on the unit circle.