Radiano

Summary

In this video lesson, Professor Kit Guedes introduces the concept of radians through the unit circle using GeoGebra software. She demonstrates how moving along the circle corresponds to measuring angles in radians, with each movement reflecting the arc length in relation to the circle's radius. The lesson covers the movement across the four quadrants, from 0 to 2π radians, and explains how to interpret both positive and negative angles. Through this visual exploration, students gain a deeper understanding of radians, the unit circle, and their application in trigonometry.

Takeaways

• 😀 The teacher introduces radians using the unit circle and a mathematical software called GEL.
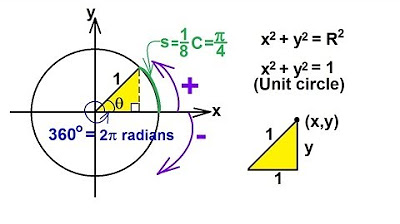
• 😀 Radians are defined as the angle formed by an arc whose length is equal to the radius of the circle.
• 😀 The lesson begins by demonstrating how to move a point around the unit circle using a slider control in the software.
• 😀 The movement along the circle shows how the angle in radians increases as the point moves counterclockwise, starting from 0 radians.
• 😀 1.05 radians corresponds to an arc length of approximately 1.05 times the radius of the circle.
• 😀 1.57 radians is approximately π/2, representing a 90-degree angle, or the first quadrant of the circle.
• 😀 3.14 radians is equivalent to π, representing half of a full revolution (180 degrees, or the second quadrant).
• 😀 4.71 radians equals 3π/2, marking three-quarters of a circle (third quadrant).
• 😀 6.28 radians equals 2π, completing a full revolution (360 degrees).
• 😀 The software visually demonstrates how the angle continues to increase beyond 2π radians, allowing students to understand multiple rotations and negative angles when moving clockwise.

Q & A

What is the main concept being taught in this video?

The main concept being taught is radians, specifically how they relate to the unit circle and how to measure angles in radians on the circle using a mathematical software.

What is the role of the 'control slider' in the demonstration?

The 'control slider' allows the user to move along the unit circle, changing the angle and observing how the corresponding arc length is measured in radians.

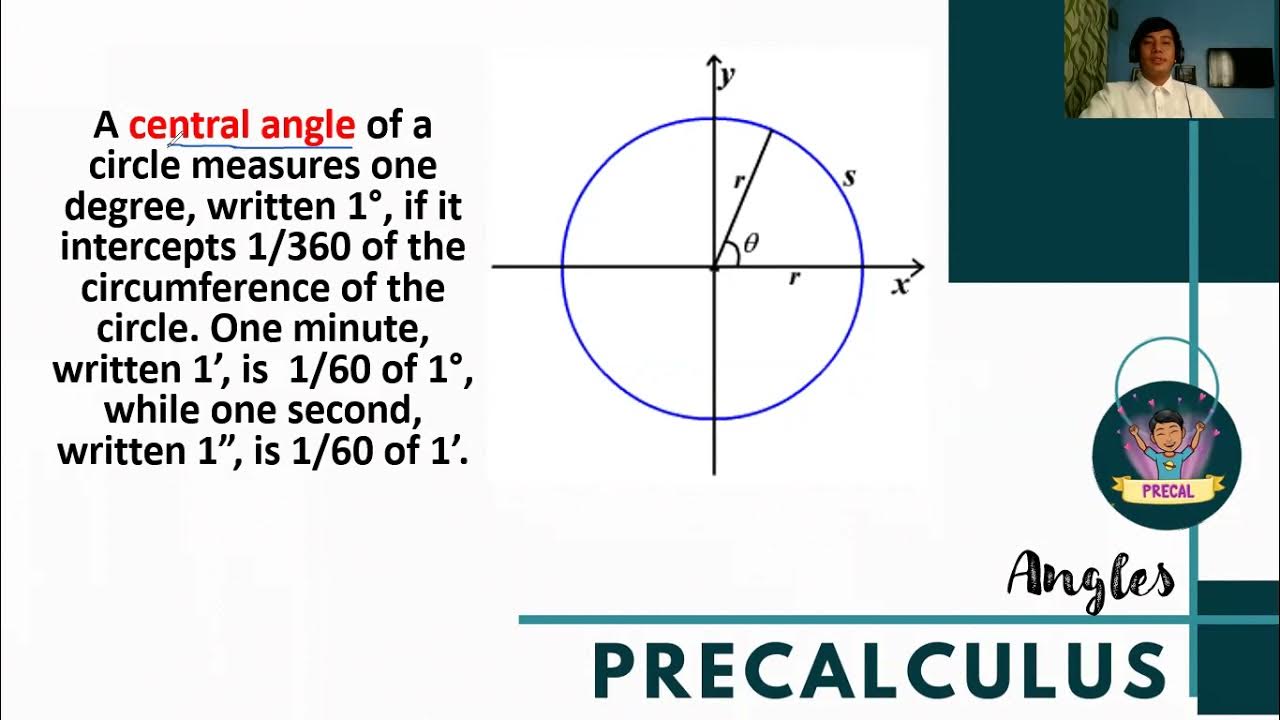
Why is the unit circle used in this explanation?

The unit circle is used because it has a radius of 1, which simplifies calculations and helps visually demonstrate the relationship between angle measures and arc lengths in radians.

What does the term 'radian' refer to in this context?

A radian is the angle subtended by an arc whose length is equal to the radius of the circle. It's a unit of angular measure.

How does the software help in understanding radians?

The software helps by visually representing the movement along the unit circle and displaying the corresponding radian measure as the angle changes, making the concept more interactive and easier to understand.

What is the significance of the angle measure of 1.57 radians?

1.57 radians corresponds approximately to 𝜋/2 radians, which is a quarter of a full circle (90 degrees). This is a key reference point for understanding the relationship between radians and angles on the unit circle.

What does the angle measure of 3.14 radians represent?

3.14 radians is approximately equal to 𝜋 radians, which is half of a full circle (180 degrees). This is an important reference for understanding angles on the unit circle.

What happens when the control slider reaches 6.28 radians?

At 6.28 radians, the control slider completes one full rotation around the unit circle, which corresponds to 2𝜋 radians (360 degrees), completing a full circle.

How does the control slider account for negative values of radians?

The control slider can account for negative values by moving in the clockwise direction around the unit circle, which is the negative direction of rotation.

What happens when the angle exceeds 2𝜋 radians?

When the angle exceeds 2𝜋 radians, the control slider begins another full rotation around the unit circle, continuing to represent additional angles beyond 360 degrees, following the same cycle.