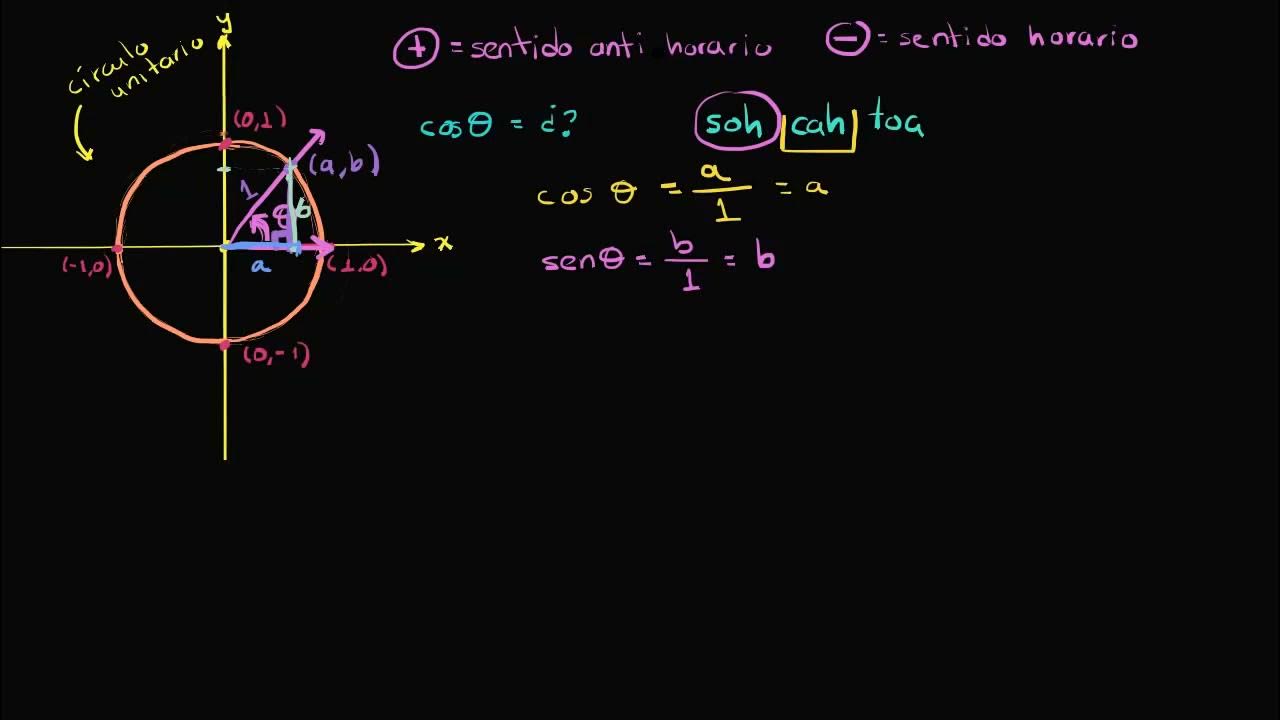Como a Trigonometria deveria ser apresentada!

Summary

Professor Julio Baldes presents trigonometry in a fresh, geometric light, starting with the unit circle instead of traditional formulas. By focusing on the relationships between angles and the circle's radius, he explains sine, cosine, tangent, secant, cotangent, and cosecant in a visual, intuitive way. The professor emphasizes the beauty of trigonometry and how understanding its geometric foundations can make learning the subject more engaging and meaningful. He encourages students to view trigonometry not as a series of formulas to memorize but as a fascinating and logical subject rooted in simple geometric principles.

Takeaways

• 😀 Trigonometry is often seen as a difficult subject, but it can be made much more approachable with the right perspective.
• 😀 The traditional focus on memorizing formulas in trigonometry can create confusion, but understanding the geometric foundations makes it easier to grasp.
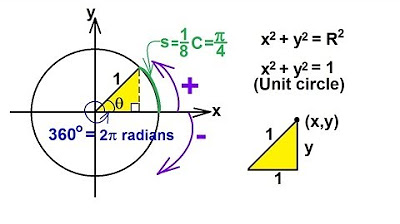
• 😀 The key to understanding trigonometry lies in understanding the relationships between the angles and sides of a triangle, which can be visualized through a unit circle.
• 😀 The sine of an angle in the unit circle is represented by the vertical distance, while the cosine is represented by the horizontal distance from the origin.
• 😀 The tangent and secant functions arise from geometric relationships in the unit circle, connecting sine and cosine.
• 😀 Trigonometric functions like cotangent and cosecant can also be understood through the unit circle and similar triangles.
• 😀 Similar triangles form the basis for deriving trigonometric identities and formulas, such as the famous Pythagorean identity.
• 😀 By recognizing the similarity between triangles, we can derive various trigonometric formulas, avoiding the need to simply memorize them.
• 😀 Trigonometry is not just about formulas; it is a beautiful subject that connects geometry and mathematics in a meaningful way.
• 😀 A geometric approach to trigonometry helps students understand the subject in a deeper and more intuitive manner, making it less of a 'nightmare.'

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is trigonometry, with a focus on understanding its concepts through a geometric approach involving circles and triangles.

How does the speaker challenge the traditional teaching of trigonometry?

The speaker challenges the traditional teaching of trigonometry by presenting it through a more intuitive, geometric lens, rather than focusing solely on memorizing formulas.

What is the significance of the circle with a radius of 1 in trigonometry?

The circle with a radius of 1 (known as the unit circle) is central to understanding trigonometric functions because it allows for the visualization of sine, cosine, and other trigonometric ratios as the intersection of a radius and a point on the circle.

How does the concept of sine and cosine emerge in the video?

The concept of sine and cosine emerges when the speaker describes a right triangle formed by the intersection of a radius (representing an angle) with the unit circle. The sine is associated with the vertical distance, and the cosine is associated with the horizontal distance.

What role do the secant and tangent functions play in the video?

The secant and tangent functions are introduced as measures derived from the interactions of the radius with the unit circle and a tangent line. These functions are shown to be related to the properties of right triangles formed in the unit circle.

Why does the speaker emphasize the importance of triangle similarity in trigonometry?

The speaker emphasizes triangle similarity because it allows for the derivation of trigonometric identities and relationships. Similar triangles have corresponding angles and proportional sides, which is key to understanding and proving trigonometric formulas.

What is the connection between triangle similarity and trigonometric identities?

The connection is that by using the similarity of triangles, one can derive various trigonometric identities. The ratios of corresponding sides in similar triangles lead to the well-known trigonometric relationships like sine, cosine, and tangent.

How does the speaker view the memorization of trigonometric formulas?

The speaker views the memorization of trigonometric formulas as unnecessary if the fundamental geometric understanding of trigonometry is established. Once the relationships between the functions are understood, the formulas can be derived easily.

What is the purpose of presenting trigonometry with geometric drawings in the video?

The purpose of presenting trigonometry with geometric drawings is to make the subject more visually and intuitively accessible, helping students appreciate the beauty of trigonometry rather than seeing it as a set of abstract, difficult formulas.

What final message does the speaker give about learning trigonometry?

The final message is that trigonometry should be presented in a way that makes it engaging and understandable, focusing on the geometric relationships rather than rote memorization. This approach helps students develop a deeper appreciation for the subject.