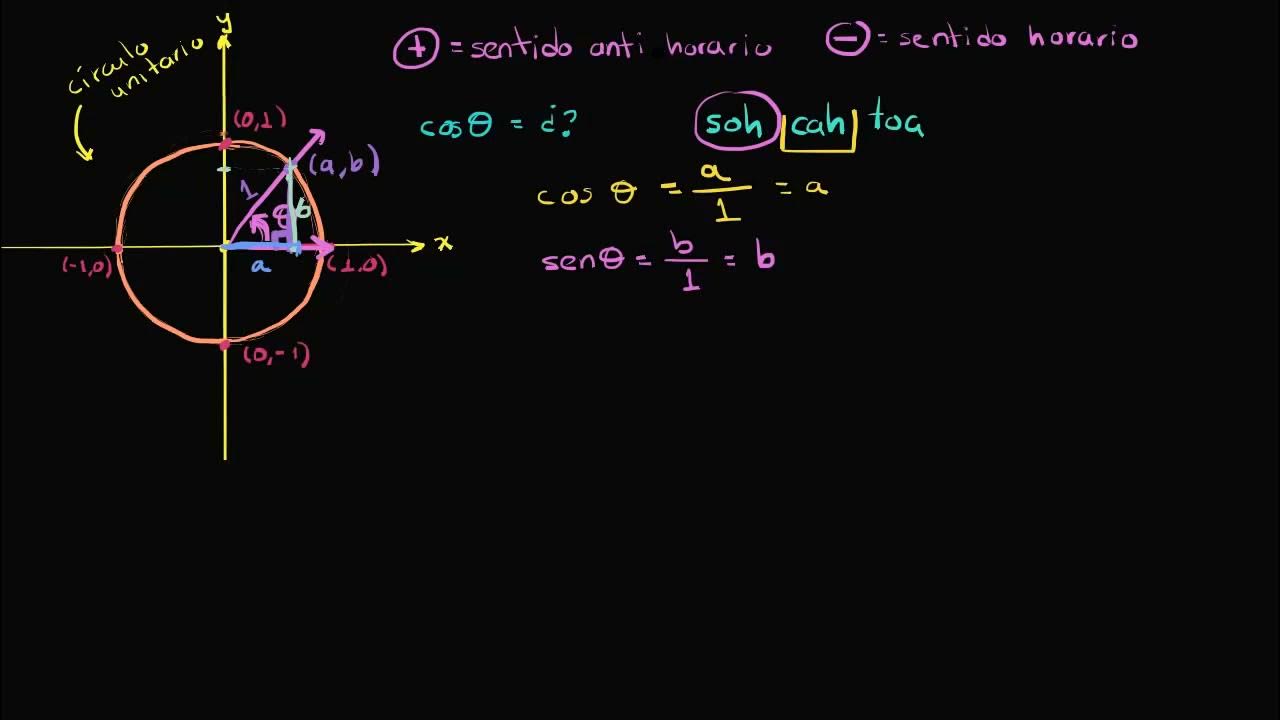De eenheidscirkel (HAVO wiskunde B)
Summary
TLDRThis video explains the unit circle and its applications in trigonometry. The speaker breaks down the concept by highlighting that the unit circle is a circle with a radius of 1 and a coordinate system inside. The video discusses key points on the unit circle and how to calculate coordinates using trigonometric functions like sine and cosine. Positive and negative rotations around the circle are also explained. The tutorial emphasizes understanding and applying formulas to find coordinates on the unit circle, making the subject more approachable with clear examples.
Takeaways
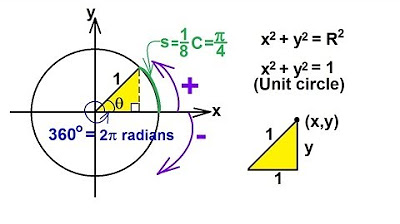
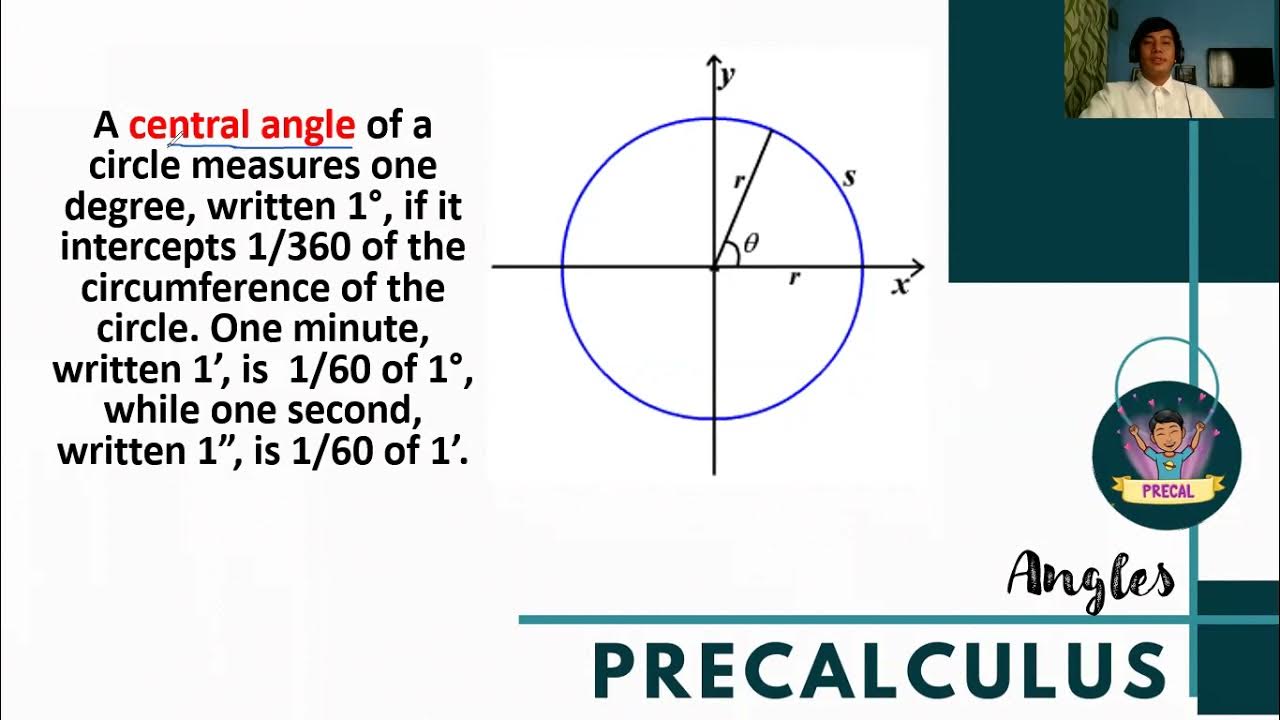
- 🔵 The unit circle is a circle with a coordinate system and a radius of 1.
- ⚪ The unit circle has four basic points: (1,0), (0,1), (-1,0), and (0,-1), representing coordinates on the x and y axes.
- 🔄 Rotation around the unit circle can be measured in angles, with counterclockwise rotation being positive and clockwise rotation being negative.
- 🧮 To calculate the coordinates of a point on the unit circle after a rotation, the x-coordinate is determined by the cosine of the angle, and the y-coordinate by the sine of the angle.
- 📐 A right-angled triangle can be formed within the unit circle, with the radius being the hypotenuse of length 1.
- 📝 The two critical formulas to remember are: x = cos(α) and y = sin(α), where α is the rotation angle.
- ⏺ The sine of an angle corresponds to the y-coordinate, and the cosine corresponds to the x-coordinate on the unit circle.
- 🌀 Positive angles are measured counterclockwise, while negative angles are measured clockwise.
- 📊 The video provides examples where the sine and cosine values of specific angles (like 90°, 180°, and -90°) are calculated based on their positions on the unit circle.
- ✅ Understanding the relationship between the unit circle, sine, and cosine is crucial for solving trigonometric problems.
Q & A
What is a unit circle?
-A unit circle is a circle with a coordinate system (axes) and a radius of 1. It is often used in trigonometry to calculate angles and trigonometric values like sine and cosine.
How is the size of the unit circle determined?
-The size of the unit circle is determined by its radius, which is always 1. This is why it is called a 'unit' circle.
What are the basic points on the unit circle?
-The basic points on the unit circle correspond to the intersections with the x and y axes: (1, 0), (0, 1), (-1, 0), and (0, -1). These represent the points at 0°, 90°, 180°, and 270° respectively.
What is the starting point for rotating a point on the unit circle?
-The starting point for rotating a point on the unit circle is (1, 0), located on the positive x-axis.
How do positive and negative rotations differ on the unit circle?
-Positive rotations move counterclockwise from the starting point (1, 0), while negative rotations move clockwise.
How do you calculate the coordinates of a point on the unit circle?
-The coordinates of a point on the unit circle can be calculated using the formulas: x = cos(α) and y = sin(α), where α is the rotation angle from the starting point.
What is the relationship between the cosine of an angle and the unit circle?
-The cosine of an angle represents the x-coordinate of a point on the unit circle corresponding to that angle.
What is the relationship between the sine of an angle and the unit circle?
-The sine of an angle represents the y-coordinate of a point on the unit circle corresponding to that angle.
What are the sine and cosine values for 180° on the unit circle?
-For 180°, the sine value (y-coordinate) is 0 and the cosine value (x-coordinate) is -1.
How can you calculate trigonometric values for negative angles on the unit circle?
-For negative angles, you rotate clockwise on the unit circle. For example, -90° corresponds to a point at (0, -1), with a sine value of -1 and a cosine value of 0.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)