Prefix Sums and Difference Array: 20 minutes of EVERYTHING you need to know

Summary

This video explores the concept of prefix sums and their applications in solving problems efficiently. It covers one-dimensional and two-dimensional prefix sums, highlighting how to calculate the sum of ranges and subgrids. The video introduces key methods like difference arrays for range updates and explains the importance of zero-based indexing and half-open intervals in competitive programming. Additionally, it touches on advanced topics like handling rotated grids and hints at extending prefix sums to three dimensions. The tutorial offers valuable insights for solving complex algorithmic problems, emphasizing practical techniques used by top programmers.

Takeaways

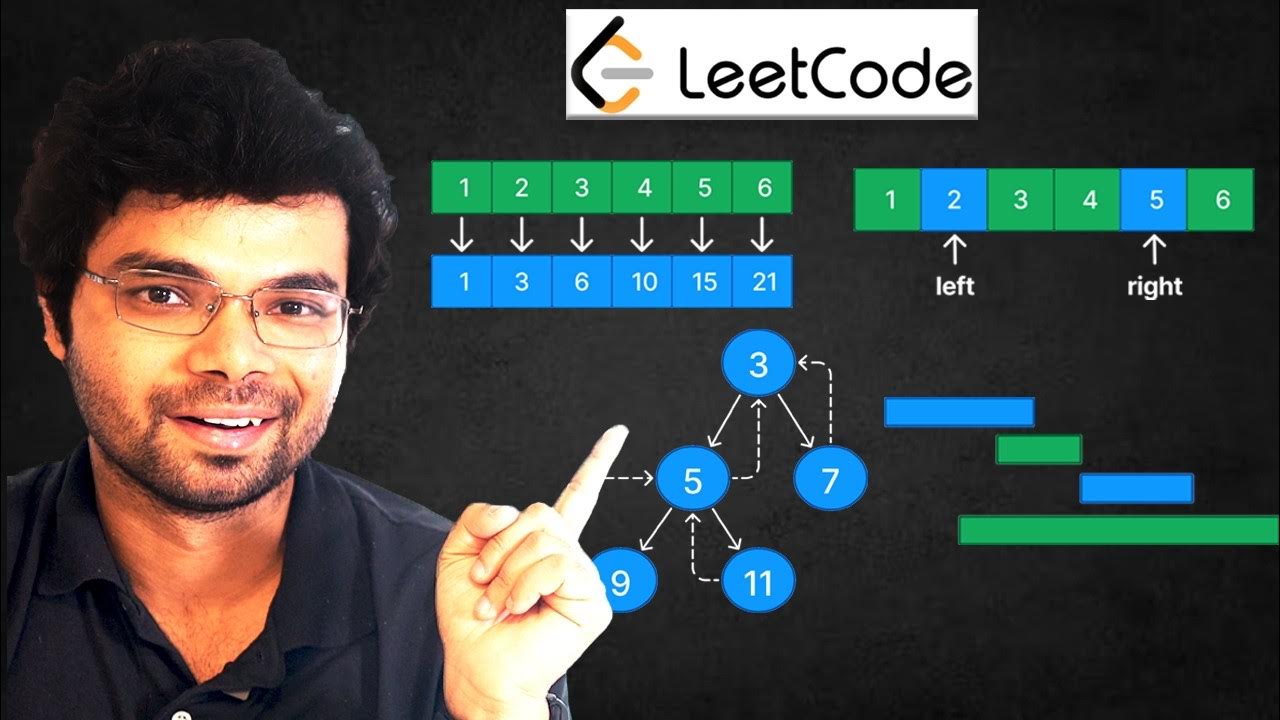
• 😀 Prefix sums help calculate range sums efficiently by using precomputed cumulative sums.
• 😀 For one-based indexing, prefix sums involve storing cumulative sums for easier calculation of range sums.
• 😀 Zero-based indexing and half-open intervals are considered more professional and commonly used in competitive programming.
• 😀 To solve range sum queries with zero-based indexing and half-open intervals, you calculate the sum as 'DP[R] - DP[L-1]'.
• 😀 The difference array method is useful for efficiently applying updates over ranges in an array without modifying every element.
• 😀 The second version of prefix sums, called the difference array, adds values to ranges incrementally using a helper array.
• 😀 For suffix updates, you can use an array to mark changes at the beginning of the range and reverse the changes just after the end of the range.
• 😀 The two-dimensional prefix sum approach calculates the sum of a subgrid by summing the DP values of the relevant areas while adjusting for overlaps.
• 😀 In two-dimensional prefix sums, the formula to compute a subgrid sum is 'DP[X2, Y2] - DP[X1-1, Y2] - DP[X2, Y1-1] + DP[X1-1, Y1-1]'.
• 😀 Adding a value to a range in a two-dimensional grid can be achieved by using four update operations to cover all relevant sections of the grid.
• 😀 To handle more complex queries, like calculating sums for diagonals or rotated grids, prefix sums can be extended with transformations like rotating the grid.

Q & A

What is the concept of prefix sums in the context of the video?

Prefix sums are a technique used to efficiently calculate the sum of elements in a subarray or subgrid. By precomputing a cumulative sum array, the sum of any range can be quickly retrieved, reducing the need for recalculating sums from scratch every time.

Why is one-based indexing considered unprofessional in competitive programming?

One-based indexing is generally considered unprofessional because it can introduce inconsistencies and errors when dealing with algorithms, especially in languages that use zero-based indexing. Zero-based indexing is more common in competitive programming because it leads to more uniform and efficient code.

How can the prefix sum technique be modified for zero-based indexing and half intervals?

In zero-based indexing and half intervals, instead of using closed intervals where both endpoints are included, half intervals include the endpoint R but exclude L. The conversion is straightforward: subtract one from L to make it zero-based, and increment R to adjust for half intervals.

What is the difference between the standard prefix sum and the difference array approach?

The standard prefix sum calculates the sum of a range directly by subtracting precomputed prefix sums. In contrast, the difference array approach is used for range updates: instead of updating all elements in a range, you mark the start and end points of changes, which is more efficient for multiple updates.

How can the difference array method be used to solve the problem of adding a value X to a subarray?

In the difference array approach, when given a query to add X to a subarray, you only update the start of the subarray by adding X, and the position just after the end of the subarray by subtracting X. This allows the range update to be efficiently applied, and the final values can be obtained by computing prefix sums on the difference array.

What is the benefit of using a two-dimensional prefix sum over a standard one-dimensional version?

The two-dimensional prefix sum allows for efficient querying of subgrids in a 2D array. By precomputing cumulative sums for both rows and columns, the sum of any rectangular subgrid can be computed in constant time, which is crucial when dealing with multiple range queries.

How can we solve the problem of finding the sum of a subgrid in a 2D prefix sum scenario?

In a 2D prefix sum scenario, you calculate the sum of the elements in the subgrid by using the inclusion-exclusion principle. The sum of the subgrid can be derived by subtracting and adding the appropriate values from the DP array, accounting for overlapping areas that were added or subtracted multiple times.

What happens when a grid is rotated, and how does that affect the sum calculations?

When a grid is rotated (e.g., by 90 degrees), the shape of the grid changes, which can complicate the calculation of sums in subgrids. One way to handle this is by rotating the grid back into a square form using a transformation, then applying standard techniques like 2D prefix sums to calculate the sum efficiently.

What is the general strategy for handling range updates in a two-dimensional array?

For range updates in a two-dimensional array, the general strategy is to decompose the update into smaller operations that can be handled efficiently. For example, a range update can be converted into multiple smaller operations on subarrays or subgrids, often using the inclusion-exclusion principle, or by utilizing difference arrays in 2D.

Can you summarize the solution to the general problem of handling range updates and queries in both 1D and 2D arrays?

The solution to range updates and queries in both 1D and 2D arrays involves preprocessing the array with prefix sums or difference arrays. For updates, only the boundary elements are modified, and then a prefix sum or cumulative sum is computed. For queries, the sums are efficiently calculated using precomputed cumulative values, either for one-dimensional arrays or for the more complex two-dimensional scenarios.