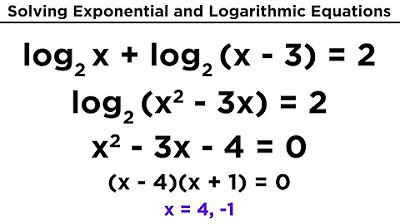Logaritmo: Introdução Parte 1 (Aula 1 de 14)

Summary

This video introduces the concept of logarithms, explaining their role in solving exponential equations. The instructor emphasizes the importance of understanding logarithmic functions for applications in mathematics exams, such as school tests and entrance exams. Key topics include the definition of logarithms, the base and exponent relationships, and how to convert between exponential and logarithmic forms. The lesson also covers the rules for manipulating logarithmic expressions and introduces natural and common logarithms. The session is aimed at providing students with foundational knowledge to tackle logarithmic problems efficiently.

Takeaways

• 😀 The topic of the lesson is logarithms, a subject that many students find challenging, but the presenter promises clear, step-by-step explanations.
• 😀 The presenter encourages viewers to subscribe to the channel to follow along with future lessons and stay updated on weekly content.
• 😀 The script begins with a brief review of exponential equations, explaining how to solve for unknown exponents when bases are equal.
• 😀 When solving exponential equations like 2^x = 8, the solution is found by recognizing that 8 is equal to 2^3, and thus x = 3.
• 😀 Another example is solving 13^x = 1/81, where 81 is factored and expressed as 13^(-4), leading to the solution x = -4.
• 😀 When bases cannot be equalized, logarithms are introduced to solve equations such as 2^x = 3, where x lies between 1 and 2.
• 😀 Logarithms provide a way to solve equations where it's difficult to directly compare exponents, allowing solutions for values of x that can't be easily calculated.
• 😀 The basic definition of a logarithm involves a base (a), an argument (b), and a result (x), with the restriction that the base (a) must be greater than 0 and not equal to 1.
• 😀 The logarithmic function is explained with the formula: if log_a(b) = x, then a^x = b. This transformation allows easier solving of complex exponentiation problems.
• 😀 The script introduces the concept of logarithms with base 10 (common logarithms), which are often abbreviated as 'log' and are commonly used in practical applications.
• 😀 The natural logarithm (ln) is also explained, with its base being the mathematical constant 'e' (approximately 2.71828), and it's particularly useful for modeling natural phenomena.

Q & A

What is the main topic of the lesson in the transcript?

The main topic of the lesson is logarithms, with a focus on understanding their properties and how they are used in solving exponential equations.

What is the first key concept introduced in the video?

The first key concept introduced is the basic definition of logarithms and how they help in solving equations where it is not possible to equalize the bases of exponential terms.

What is the relationship between exponential equations and logarithms?

Logarithms are introduced as a tool for solving exponential equations where the bases cannot be easily equalized. Logarithms help in finding the exponent (x) that satisfies such equations.

Why do students often struggle with logarithms according to the speaker?

According to the speaker, many students find logarithms difficult and often dislike the topic because it introduces abstract concepts like working with exponents and bases in ways that may not be intuitive.

How are exponential equations solved in the transcript?

Exponential equations are solved by equating the exponents when the bases are the same. If the bases are not the same, logarithms are used to solve for the unknown exponent.

What method is demonstrated to solve an exponential equation like 2^x = 8?

The method demonstrated involves recognizing that 8 is equal to 2^3. Once the bases are the same, the exponents are set equal to each other, resulting in x = 3.

What happens when the bases in an exponential equation cannot be equalized?

When the bases cannot be equalized, logarithms are used to solve the equation by finding the exponent that satisfies the equation, even when the bases are different.

How is the logarithmic operation explained in the lesson?

The logarithmic operation is explained as the inverse of an exponential function. For example, log_b(x) equals y means that b raised to the power of y equals x.

What are the base restrictions for logarithms mentioned in the transcript?

The base of a logarithm must be greater than zero and cannot be equal to one. This is because the logarithmic function requires a positive base, and a base of 1 does not produce unique results.

What are natural logarithms, and why are they significant?

Natural logarithms use the base 'e', a constant approximately equal to 2.71828. They are important because many natural phenomena, such as growth processes, are modeled using exponential functions with this base.