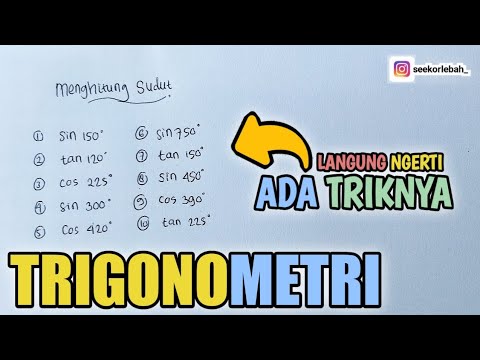
Tanda Fungsi Trigonometri Tiap Kuadran | Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka

Summary

In this video, the instructor explains the concept of trigonometric functions, specifically focusing on how to determine their signs in different quadrants using the unit circle. Beginning with a review of basic trigonometric ratios from previous lessons, the video walks through the method of analyzing the signs of sine, cosine, and tangent functions in the first, second, third, and fourth quadrants. The key idea is that the signs of these functions depend on the quadrant, and the unit circle helps illustrate and validate these relationships. The lesson is tailored for students in 11th-grade mathematics, part of the Merdeka curriculum.

Takeaways

• 😀 The lesson focuses on understanding trigonometric functions for advanced mathematics at the 11th grade level, using the unit circle concept to simplify learning.
• 😀 The unit circle is a circle with a radius of one unit, used to define the values of trigonometric functions.
• 😀 In the unit circle, the equation of the circle is x^2 + y^2 = 1, and each point on the circle represents a coordinate (x, y).
• 😀 The script emphasizes the importance of combining the unit circle concept with previously learned trigonometric ratios from class 10, such as sin, cos, and tan.
• 😀 Sin, Cos, and Tan functions are defined as the ratios of the sides of a right triangle, where sin is the ratio of the opposite side to the hypotenuse, cos is adjacent over hypotenuse, and tan is the opposite side over the adjacent side.
• 😀 The video explains how to determine the signs of trigonometric functions in each of the four quadrants of the unit circle, starting with quadrant 1 where all functions are positive.
• 😀 In quadrant 2 (from 90° to 180°), sin is positive while cos and tan are negative.
• 😀 In quadrant 3 (from 180° to 270°), tan is positive while sin and cos are negative.
• 😀 In quadrant 4 (from 270° to 360°), cos is positive while sin and tan are negative.
• 😀 The script provides step-by-step examples of how to calculate the values and signs of trigonometric functions in each quadrant using the unit circle and the corresponding right triangles.

Q & A

What is the main focus of the lesson in this video?

The main focus of the lesson is on trigonometric functions, specifically using the unit circle to understand how the signs of trigonometric functions vary across different quadrants.

What is the unit circle and how is it used in this lesson?

The unit circle is a circle with a radius of one unit. It is used in this lesson to help visualize and understand trigonometric functions, such as sine, cosine, and tangent, by examining their values at different points on the circle.

What are the key concepts introduced from the previous lesson in this video?

The key concepts from the previous lesson include the basic trigonometric ratios (sine, cosine, and tangent) derived from a right triangle, which are then linked with the unit circle in this lesson.

How does the lesson explain the connection between the unit circle and trigonometric functions?

The lesson explains that the unit circle helps determine the values of trigonometric functions by considering a right triangle formed within the circle, with the hypotenuse as the radius (equal to 1) and the sides representing the sine, cosine, and tangent values.

How is the sign of trigonometric functions determined in each quadrant?

The sign of trigonometric functions in each quadrant is determined by the coordinates of the points on the unit circle. In the first quadrant, all functions are positive; in the second, only sine is positive; in the third, only tangent is positive; and in the fourth, only cosine is positive.

What is the purpose of using a right triangle within the unit circle?

The purpose of using a right triangle within the unit circle is to apply the trigonometric ratios (sine, cosine, and tangent) to the points on the circle, making it easier to understand how these ratios behave in different quadrants.

What is the interval for the first quadrant, and what are the signs of the functions there?

The interval for the first quadrant is from 0° to 90°. In this quadrant, all trigonometric functions (sine, cosine, and tangent) are positive.

How does the second quadrant differ from the first in terms of trigonometric functions?

In the second quadrant (from 90° to 180°), only sine is positive, while cosine and tangent are negative. This is due to the negative x-coordinate in the second quadrant.

What is the unique characteristic of the third quadrant regarding trigonometric functions?

In the third quadrant (from 180° to 270°), only tangent is positive, while sine and cosine are negative. This is because both the x- and y-coordinates are negative in this quadrant.

What happens in the fourth quadrant with regard to the signs of trigonometric functions?

In the fourth quadrant (from 270° to 360°), only cosine is positive, while sine and tangent are negative. This is due to the positive x-coordinate and negative y-coordinate in this quadrant.