CARA MENGHITUNG SUDUT TRIGONOMETRI‼️
Summary
TLDRThis video tutorial focuses on teaching high school students the fundamentals of trigonometry, particularly how to calculate angles using sine, cosine, and tangent functions. The instructor explains key concepts like trigonometric quadrants, the even (genap) and odd (ganjil) methods for handling angles, and the importance of memorizing special angles such as 30°, 45°, 60°, and 90°. Through practical examples, viewers learn how to apply these methods for accurate angle calculations and understand the rules for determining the signs of trigonometric functions in different quadrants.
Takeaways
- 😀 The importance of praying is emphasized before engaging in any activities, including studying mathematics.
- 😀 The video explains the basics of trigonometry, which is important for both high school and college students.
- 😀 Understanding the four quadrants of the unit circle is crucial in solving trigonometric problems.
- 😀 The signs of trigonometric functions (sine, cosine, tangent) change depending on the quadrant in which the angle lies.
- 😀 The even method (using angles of 180° and 360°) and odd method (using angles of 90° and 270°) are two approaches for solving trigonometric problems.
- 😀 Special angles in trigonometry (30°, 45°, 60°, 90°) should be memorized for quick calculation of sine, cosine, and tangent values.
- 😀 The relationship between sine, cosine, and tangent can be learned by memorizing the values for special angles.
- 😀 The example of calculating Sin 150° is used to demonstrate how the even method works in practice.
- 😀 The video provides a step-by-step breakdown of how to use the even and odd methods to calculate trigonometric values for specific angles.
- 😀 Practical examples like Sin 150°, Tan 120°, and Cos 225° show how to apply trigonometric concepts in real calculations.
Q & A
What is the significance of understanding trigonometric angles in high school mathematics?
-Understanding trigonometric angles is crucial as it forms the foundation for advanced mathematics, both in high school and in higher education, including college-level courses. Mastery of these concepts helps in solving various real-world problems in engineering, physics, and other fields.
What are the basic trigonometric functions mentioned in the script?
-The basic trigonometric functions mentioned in the script are sine (sin), cosine (cos), and tangent (tan). These functions are fundamental in trigonometry and are used to calculate angles and sides of triangles.
What are the four quadrants in the unit circle, and how do they relate to trigonometric functions?
-The four quadrants are numbered 1 through 4, starting from the positive x-axis and moving counterclockwise. In quadrant 1, all trigonometric functions are positive. In quadrant 2, sine is positive, while cosine and tangent are negative. In quadrant 3, tangent is positive, while sine and cosine are negative. In quadrant 4, cosine is positive, while sine and tangent are negative.
What is the difference between the 'genap' (even) and 'ganjil' (odd) methods in trigonometry?
-The 'genap' (even) method is used for angles like 180° and 360°, where the function remains unchanged. In contrast, the 'ganjil' (odd) method is used for angles like 90° and 270°, where the sine and cosine functions switch. For example, sin(90°) becomes cos(0°) and vice versa.
What are the 'special angles' mentioned in the script, and why are they important?
-The special angles are 0°, 30°, 45°, 60°, and 90°. These angles are important because their sine, cosine, and tangent values are well-known and easy to memorize. They form the basis for solving many trigonometric problems.
How can you calculate sin(150°) using the genap method?
-To calculate sin(150°), you can use the genap method by subtracting 30° from 180° (since 180° is closer to 150°). This gives sin(150°) = sin(30°), which equals 1/2.
What role does the unit circle play in understanding trigonometric functions?
-The unit circle is fundamental in visualizing how trigonometric functions behave. It helps in determining the signs of the trigonometric functions based on the quadrant in which the angle lies, making it easier to solve trigonometric problems.
What is the method for calculating sin(300°)?
-To calculate sin(300°), you can use the genap method by subtracting 60° from 360° (since 360° is closer to 300°). This gives sin(300°) = -sin(60°), which equals -√3/2.
What happens when you use the ganjil method to calculate sin(150°)?
-Using the ganjil method for sin(150°) involves rewriting 150° as 90° + 60°. This results in sin(150°) = cos(60°), which equals 1/2.
Why is it important to memorize the special angles and their corresponding trigonometric values?
-Memorizing the special angles and their corresponding values is important because it allows students to quickly and accurately solve problems involving trigonometric functions without relying on a calculator or complicated formulas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Vektor Fisika • Part 1: Pengantar Trigonometri Dasar

Matematika SMA - Trigonometri (3) -Sistem Kuadran, Relasi Sudut Trigonometri (A)

Media Pembelajaran Trigonometri || Jari Trigonometri (Jargonometri)
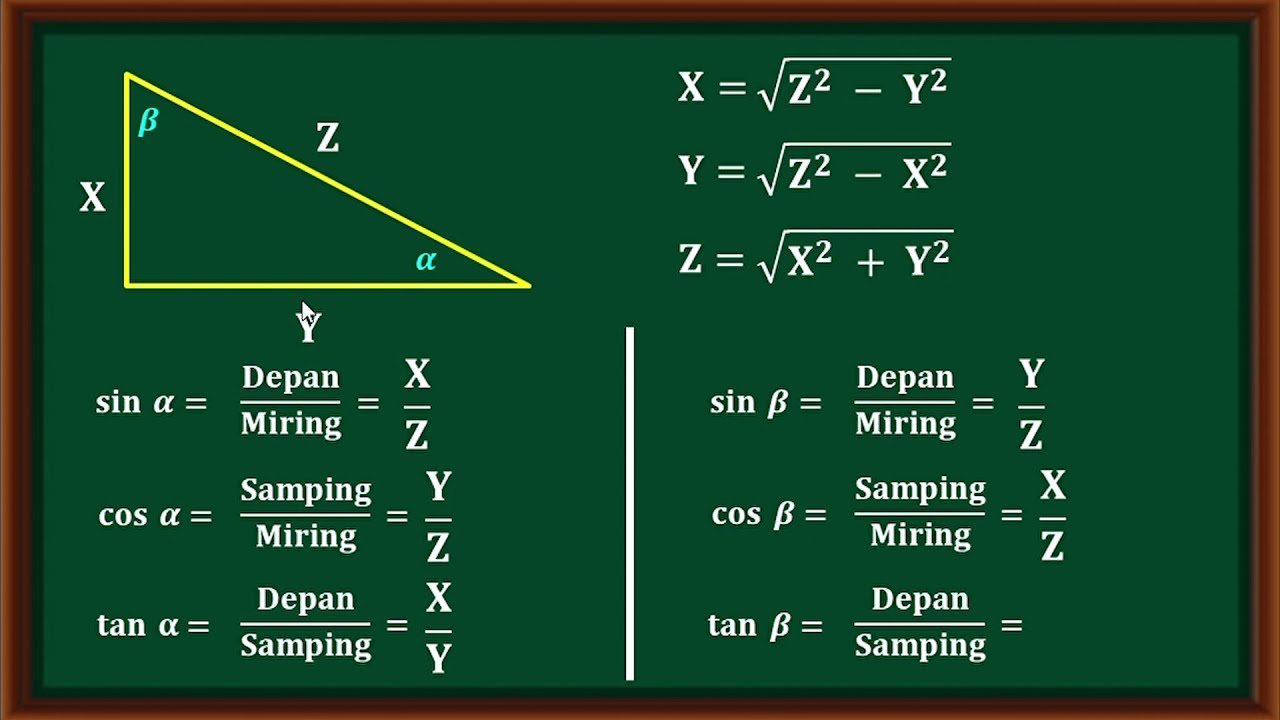
Materi dan soal pembahasan Perbandingan trigonometri dari suatu sudut pada segitiga siku-siku.

Matematika SMA - Trigonometri (1) - Pengenalan Trigonometri, Perbandingan Trigonometri (A)

Trigonometry For Beginners!
5.0 / 5 (0 votes)