KESEBANGUNAN PADA SEGITIGA SIKU-SIKU
Summary
TLDRThis educational video teaches viewers about the concept of similarity in right-angled triangles. It explains key formulas for calculating the relationships between the sides of such triangles, including how to derive them from the proportional relationships of corresponding sides. Through clear explanations, viewers are guided on how these formulas are developed, helping them understand rather than just memorize. The video also demonstrates the practical application of these formulas to solve geometry problems, encouraging viewers to practice and calculate side lengths with examples provided.
Takeaways
- 😀 The video focuses on teaching how to calculate the similarity in right-angled triangles.
- 😀 The key formulas for right triangle similarity are introduced: ad² = BD * CD, ab² = BD * BC, and ac² = CD * BC.
- 😀 The video stresses the importance of understanding the derivation of formulas rather than just memorizing them.
- 😀 The speaker explains that right triangles in a larger triangle are similar, and this similarity leads to proportional relationships between their corresponding sides.
- 😀 To derive ad² = BD * CD, the speaker compares corresponding sides of triangles ABD and ACD.
- 😀 Similarly, ab² = BD * BC is derived from comparing corresponding sides of triangles ABC and ABD.
- 😀 The formula ac² = CD * BC comes from the comparison of sides in triangles ABC and ACD.
- 😀 The video emphasizes that understanding the relationship between the sides of similar triangles is key to deriving these formulas.
- 😀 A practical example is provided where the formulas are used to calculate side lengths: NK = 12 cm and KL = 15 cm.
- 😀 The video encourages viewers to practice calculating other side lengths, offering a challenge to determine MK on their own.
- 😀 The speaker concludes with a positive sign-off, encouraging continued learning and understanding of geometry concepts.
Q & A
What is the focus of the video?
-The video focuses on teaching the concept of similarity in right-angled triangles, including deriving and understanding key formulas for such triangles.
Why is it important to understand the concept of similarity before memorizing formulas?
-Understanding the concept of similarity helps to grasp how the formulas are derived, ensuring that they can be applied correctly even if the formulas are forgotten.
What is the first formula mentioned in the video for right-angled triangles?
-The first formula mentioned is ad² = BD * CD, where ad is the base of triangle ABD, BD is the height, and CD is the base of triangle ACD.
How is the formula ad² = BD * CD derived?
-This formula is derived by comparing the corresponding sides of two similar right-angled triangles, triangle ABD and triangle ACD, and then using cross-multiplication to derive the relationship.
What is the second formula discussed in the video?
-The second formula is ab² = BD * BC, where ab is the hypotenuse of triangle ABD, BD is the height, and BC is the hypotenuse of triangle ABC.
How is the formula ab² = BD * BC derived?
-The formula is derived by comparing the corresponding sides of triangle ABC and triangle ABD, and then using cross-multiplication of the similar sides.
What is the third formula presented in the video?
-The third formula is ac² = CD * BC, where ac is the hypotenuse of triangle ABC, CD is the base of triangle ACD, and BC is the hypotenuse of triangle ABC.
How is the formula ac² = CD * BC derived?
-This formula is derived by comparing the corresponding sides of triangle ABC and triangle ACD, then using cross-multiplication to form the equation.
What example problem is solved in the video, and what is its focus?
-The video solves an example involving three line segments: NK, KL, and MK. The focus is on applying the previously discussed formulas to find the lengths of these segments.
How is the length of NK determined in the example problem?
-The length of NK is calculated using the formula nk² = MN * LN. By substituting MN = 16 and LN = 9, we get nk² = 144, so NK = 12 cm.
How is the length of KL determined in the example problem?
-The length of KL is calculated using the formula kl² = LN * LM. By substituting LN = 9 and LM = 25, we get kl² = 225, so KL = 15 cm.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

KESEBANGUNAN BANGUN DATAR matematika SMP kelas VII Kurikulum Merdeka revisi 2022 Bab 5
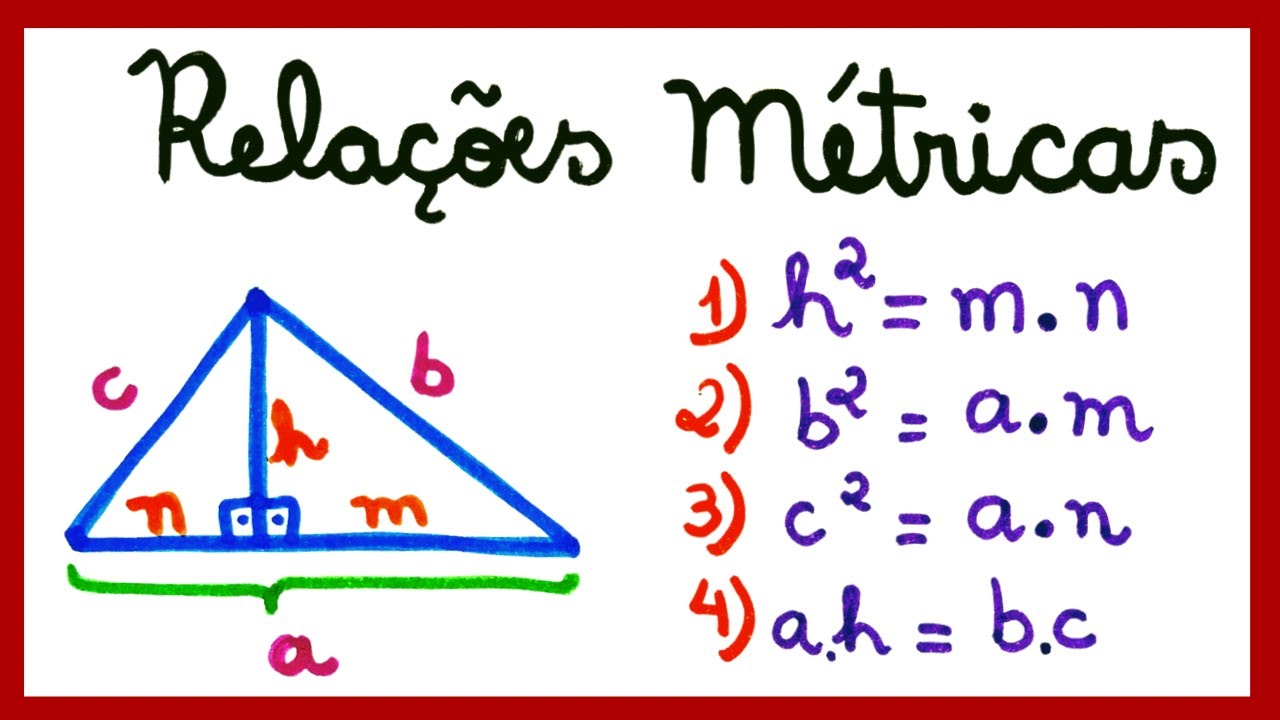
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO!!
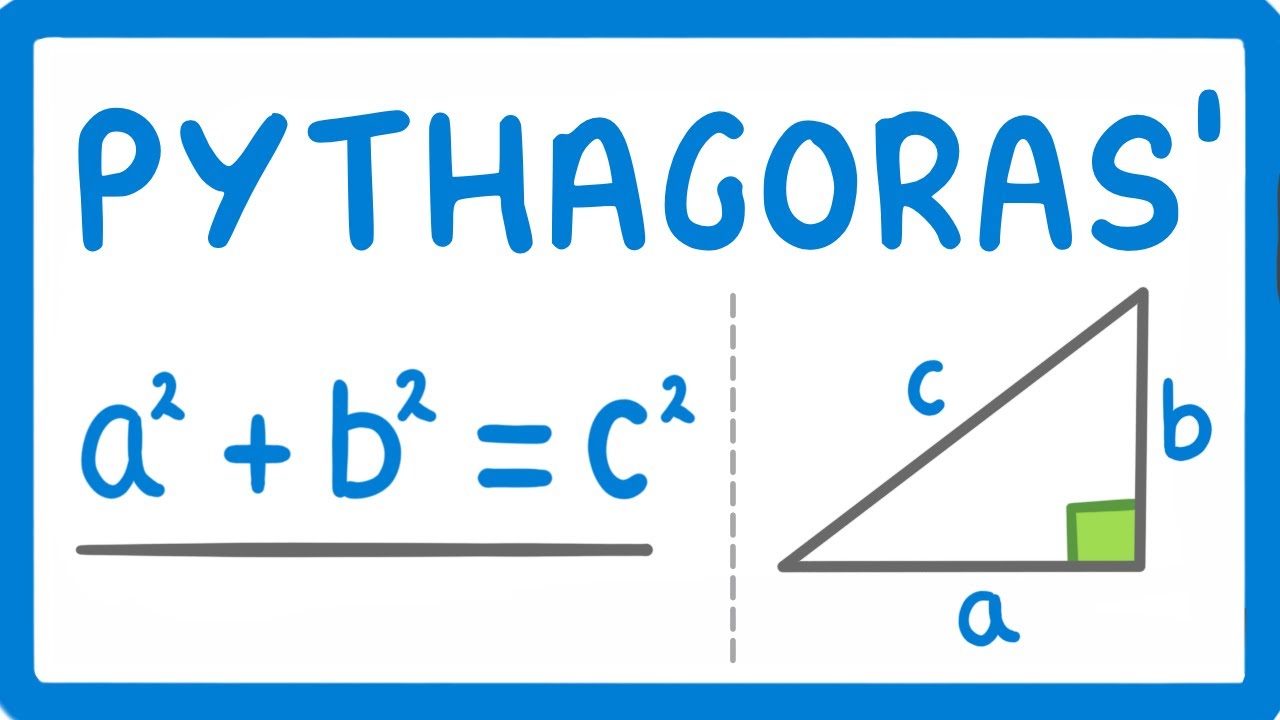
GCSE Maths - Pythagoras' Theorem And How To Use It #120

Teorema Pythagoras [Part 4] - Menentukan Perbandingan Sisi Segitiga Siku-siku
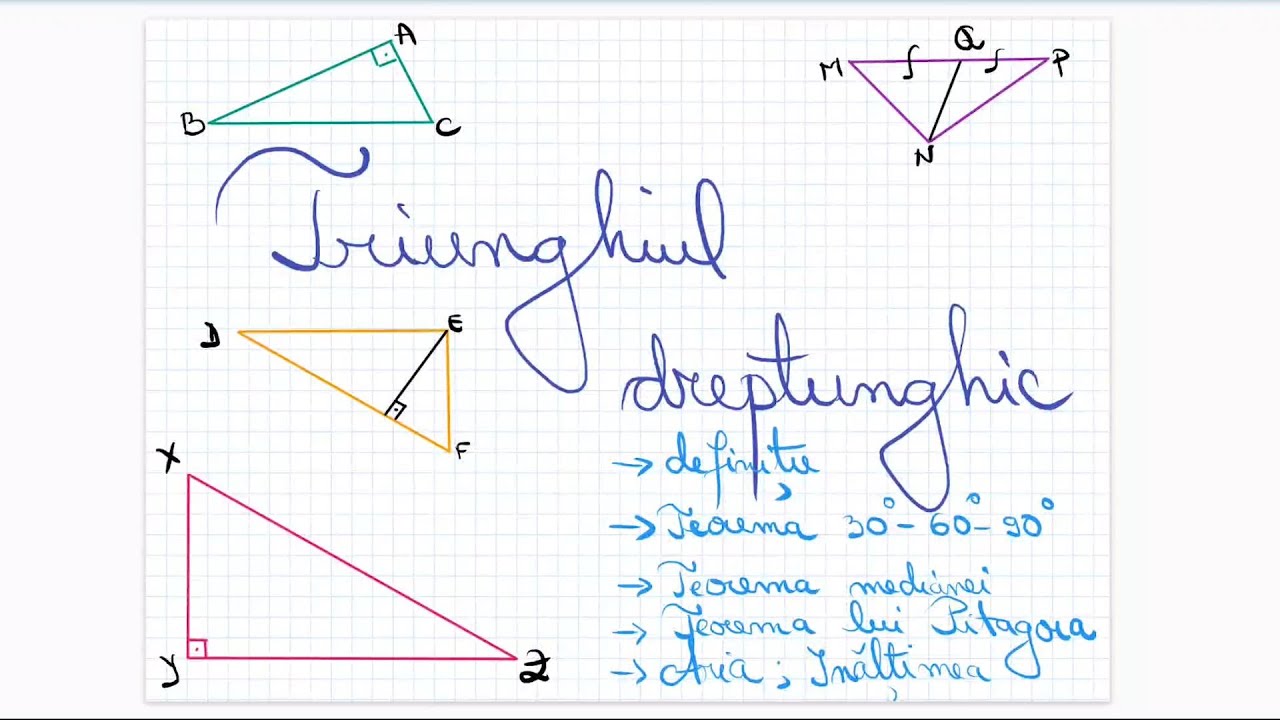
Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie

GCSE Maths - Pythagoras' Theorem And How To Use It #120
5.0 / 5 (0 votes)