RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO!!
Summary
TLDRIn this video, Professor Michele Amorim teaches the concept of metric relations in right-angled triangles. She introduces key terms such as the hypotenuse, catheti, projections, and height, explaining their significance in solving geometric problems. The video covers essential formulas derived from triangle similarity, including the Pythagorean Theorem, and demonstrates how to apply these formulas in various problems. The session encourages understanding through step-by-step problem-solving and elimination strategies, offering a practical approach to mastering right triangle properties. The teacher also hints at future lessons focusing on more advanced topics like the Pythagorean Theorem.
Takeaways
- 😀 Understanding the basic elements of a right triangle: hypotenuse, catetos (legs), and height.
- 😀 The hypotenuse is the side opposite the right angle, while the catetos are the sides forming the right angle.
- 😀 Projections of the catetos onto the hypotenuse are essential for solving problems involving right triangles.
- 😀 The height is defined as the segment that forms a 90° angle with the hypotenuse.
- 😀 Metric relationships connect the sides, height, and projections of the right triangle, offering formulas for problem-solving.
- 😀 One key formula is: Height squared = Product of the projections of the catetos on the hypotenuse.
- 😀 Another important formula is: Cateto squared = Product of hypotenuse and its projection on the cateto.
- 😀 The relationship between the hypotenuse and the height can be expressed as: Hypotenuse * Height = Product of the two catetos.
- 😀 Simplifying complex problems involves identifying the appropriate formula based on known values and eliminating unnecessary variables.
- 😀 The Pythagorean theorem is a critical tool for solving right triangle problems, though it is saved for a separate video.
- 😀 The process of solving problems becomes faster with practice and by understanding how each letter in a formula corresponds to the actual segments of the triangle.
Q & A
What is the focus of this lesson?
-The lesson focuses on the metric relationships in right-angled triangles, specifically the relationships between the sides and how they can be represented through formulas.
What is the definition of a right triangle as mentioned in the script?
-A right triangle is a triangle that contains a 90-degree angle. The side opposite this right angle is called the hypotenuse.
What are the names of the sides in a right triangle?
-In a right triangle, there are two legs called 'catetos' (the sides that form the 90-degree angle), and one hypotenuse (the side opposite the right angle).
What is the importance of labeling the sides of the triangle with letters?
-Labeling the sides of the triangle with letters simplifies solving problems. It allows the use of formulas instead of describing each side in full every time.
How is the hypotenuse typically denoted in formulas?
-The hypotenuse is typically denoted by the letter 'a' in formulas.
What are the projections in a right triangle?
-Projections refer to the parts of the hypotenuse that correspond to the projections of the legs (catetos) onto the hypotenuse, denoted as 'm' and 'n' for the two catetos.
What is the first key formula for metric relations in right triangles?
-The first key formula states that the square of the height (h²) is equal to the product of the two projections (m * n).
How do you calculate the length of the hypotenuse using the projections?
-You can calculate the hypotenuse by adding the lengths of the two projections (m + n), as the hypotenuse is the sum of these projections.
What is the relationship between the catetos and the hypotenuse in a right triangle?
-The relationship between the catetos and the hypotenuse is given by the Pythagorean theorem, where the square of the hypotenuse (a²) equals the sum of the squares of the two catetos (b² + c²).
How can the height of the triangle be related to its catetos and projections?
-The height (h) can be related to the catetos and their projections through the formula h² = m * n, where m and n are the projections of the catetos onto the hypotenuse.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

KESEBANGUNAN PADA SEGITIGA SIKU-SIKU
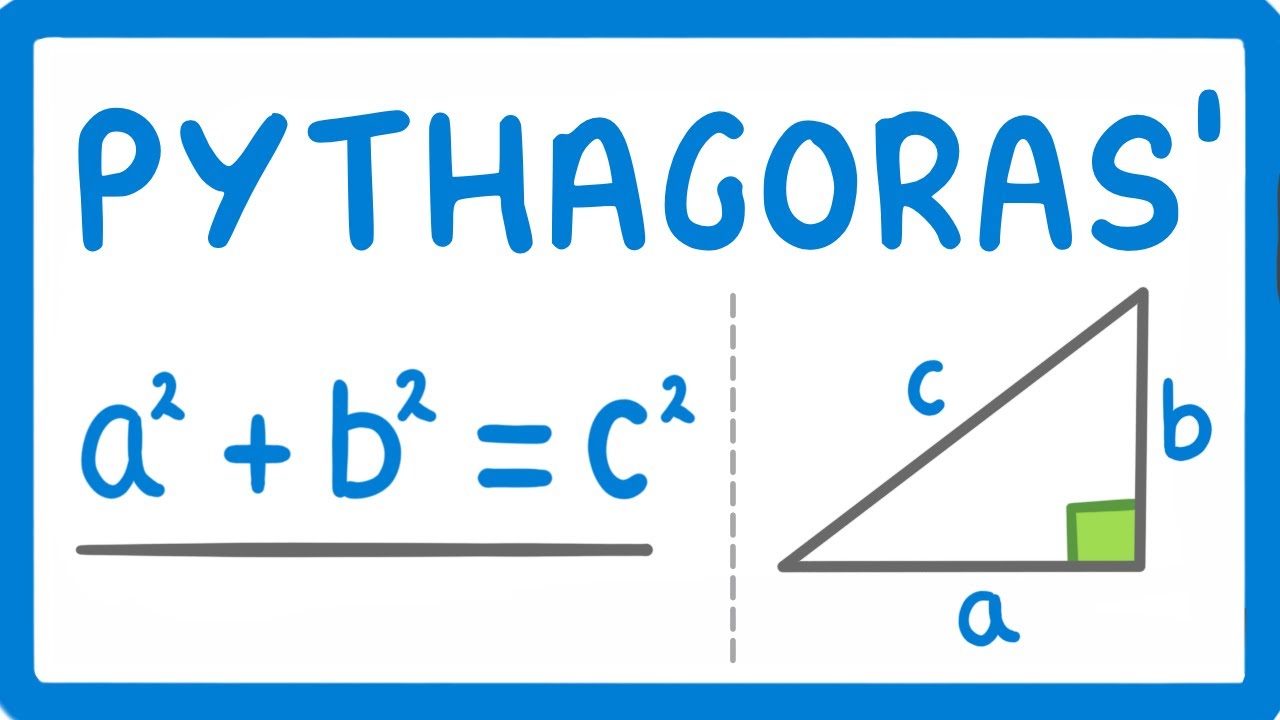
GCSE Maths - Pythagoras' Theorem And How To Use It #120
Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie
¿Qué son las razones trigonométricas? @MatematicasprofeAlex

Teorema Pythagoras [Part 1] - Menentukan Panjang Salah Satu Sisi Pada Segitiga Siku-siku

Teorema Pythagoras [Part 4] - Menentukan Perbandingan Sisi Segitiga Siku-siku
5.0 / 5 (0 votes)