GCSE Maths - Pythagoras' Theorem And How To Use It #120

Summary

This educational video script teaches viewers how to apply Pythagoras' theorem to find missing side lengths in right-angled triangles. It emphasizes the importance of identifying a right angle and knowing two side lengths to use the theorem. The script explains the formula a^2 + b^2 = c^2, where 'c' is the hypotenuse. Examples are provided to demonstrate the process of labeling sides, plugging values into the equation, and solving for the unknown side. The video aims to clarify common points of confusion and encourages practice with provided problems.

Takeaways

• 📐 Use Pythagoras' theorem for right-angle triangles where one angle is 90 degrees.
• ✅ Ensure you know the lengths of two sides to apply the theorem.
• 🔍 Identify the missing side, which will be calculated using the theorem.
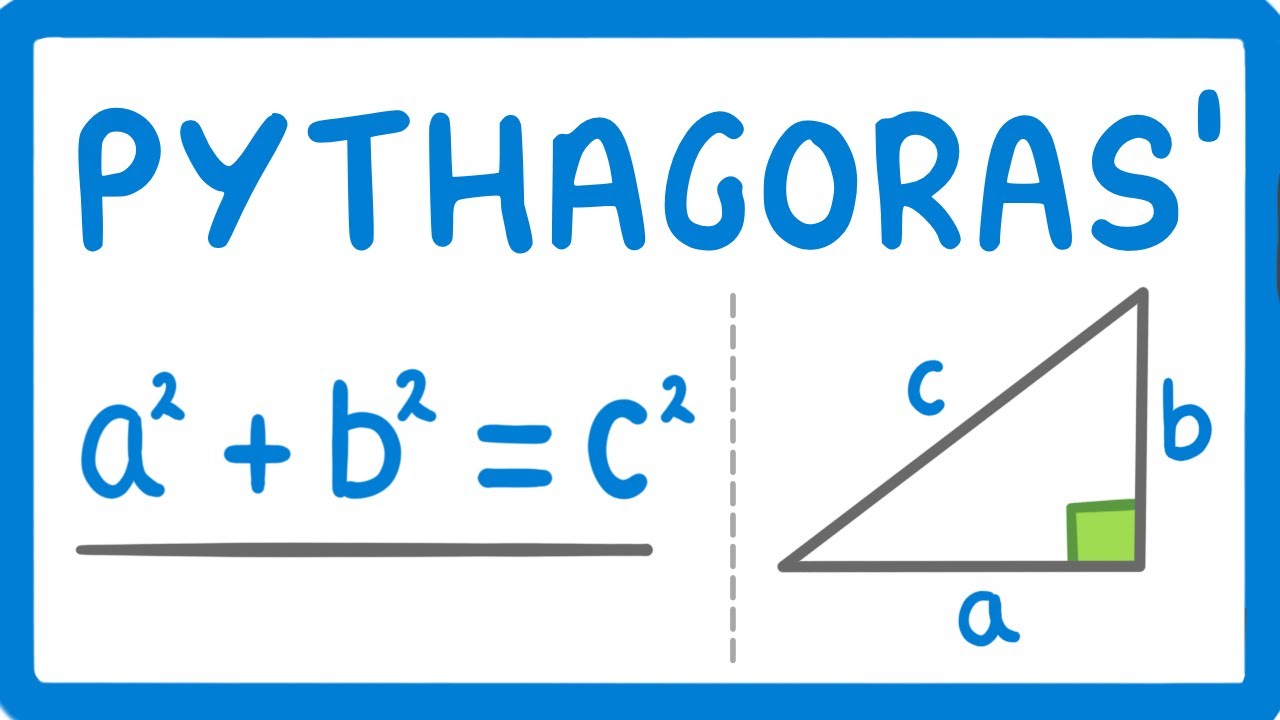
• 💡 Memorize the Pythagorean equation: a^2 + b^2 = c^2, where c is the hypotenuse.
• 📏 Label the sides correctly as a, b, and c (hypotenuse) for easier calculation.
• 🔢 Substitute the known side lengths into the equation and solve for the unknown.
• 📉 Use a calculator for squaring and square rooting when solving for unknowns.
• 📋 Practice by applying the theorem to different triangles with varying side lengths.
• 📝 Pay attention to how questions label the sides and angles to correctly identify a, b, and c.
• 👨‍🏫 The video provides a step-by-step guide to solving problems using Pythagoras' theorem.

Q & A

What is the main topic of the video?

The main topic of the video is how to use Pythagoras' theorem to calculate the missing length of a triangle.

What is a prerequisite for using Pythagoras' theorem as described in the video?

A prerequisite for using Pythagoras' theorem is that the triangle must be a right-angle triangle, meaning it has a 90-degree angle.

According to the video, how many side lengths must you know to apply Pythagoras' theorem?

You must know the lengths of two sides to apply Pythagoras' theorem.

What is the equation for Pythagoras' theorem as mentioned in the video?

The equation for Pythagoras' theorem is a^2 + b^2 = c^2, where c is the hypotenuse and a and b are the other two sides.

What is the significance of the hypotenuse in the context of Pythagoras' theorem?

In the context of Pythagoras' theorem, the hypotenuse is the longest side of the triangle, always opposite the right angle.

Can the order of sides a and b be switched in the Pythagoras' theorem equation?

Yes, the order of sides a and b can be switched in the Pythagoras' theorem equation, as long as c is correctly identified as the hypotenuse.

How do you solve for the unknown side in the equation 4^2 + 3^2 = c^2 as per the video?

You simplify the equation to 16 + 9 = c^2, then to 25 = c^2, and finally take the square root of both sides to find c = 5.

What is the process for solving a problem where the unknown side is the hypotenuse, as shown in the video?

The process involves labeling the sides as a, b, and c, plugging the known values into the equation a^2 + b^2 = c^2, and then solving for c.

How does the video handle questions where the triangle is labeled with corner names like x, y, and z?

The video suggests ignoring the labeled corner names and focusing on labeling the sides as a, b, and c for the purpose of applying Pythagoras' theorem.

What is the final step to find the length of the unknown side after setting up the equation according to the video?

The final step is to solve the equation by performing the necessary mathematical operations, such as squaring and taking square roots, to isolate the unknown side.