Incenter, Circumcenter, Orthocenter & Centroid of a Triangle - Geometry
Summary
TLDRThis educational video script delves into the geometric centers of a triangle, explaining the incenter found by angle bisectors, the centroid located at the medians' intersection, the orthocenter where altitudes meet, and the circumcenter at the perpendicular bisectors' convergence. It clarifies the position of these centers in acute, right, and obtuse triangles, providing a comprehensive review of their identification and properties.
Takeaways
- 📐 The incenter of a triangle is found at the intersection of the three angle bisectors and is always inside the triangle.
- 🔵 The incenter is the center of the inscribed circle of the triangle, which touches all three sides.
- 📏 The centroid, found at the intersection of the three medians, is always inside the triangle and divides each median into segments with a ratio of 2:1.
- 📍 The orthocenter is the intersection of the three altitudes and can lie inside, on, or outside the triangle depending on whether it's acute, right, or obtuse.
- 🔺 In an acute triangle, the orthocenter is inside; in a right triangle, it's at the right angle vertex; and in an obtuse triangle, it's outside.
- 🌐 The circumcenter is the intersection of the three perpendicular bisectors and can also be inside, on, or outside the triangle depending on its type.
- 🔶 For acute triangles, the circumcenter is inside; for right triangles, it's at the midpoint of the hypotenuse; and for obtuse triangles, it's outside.
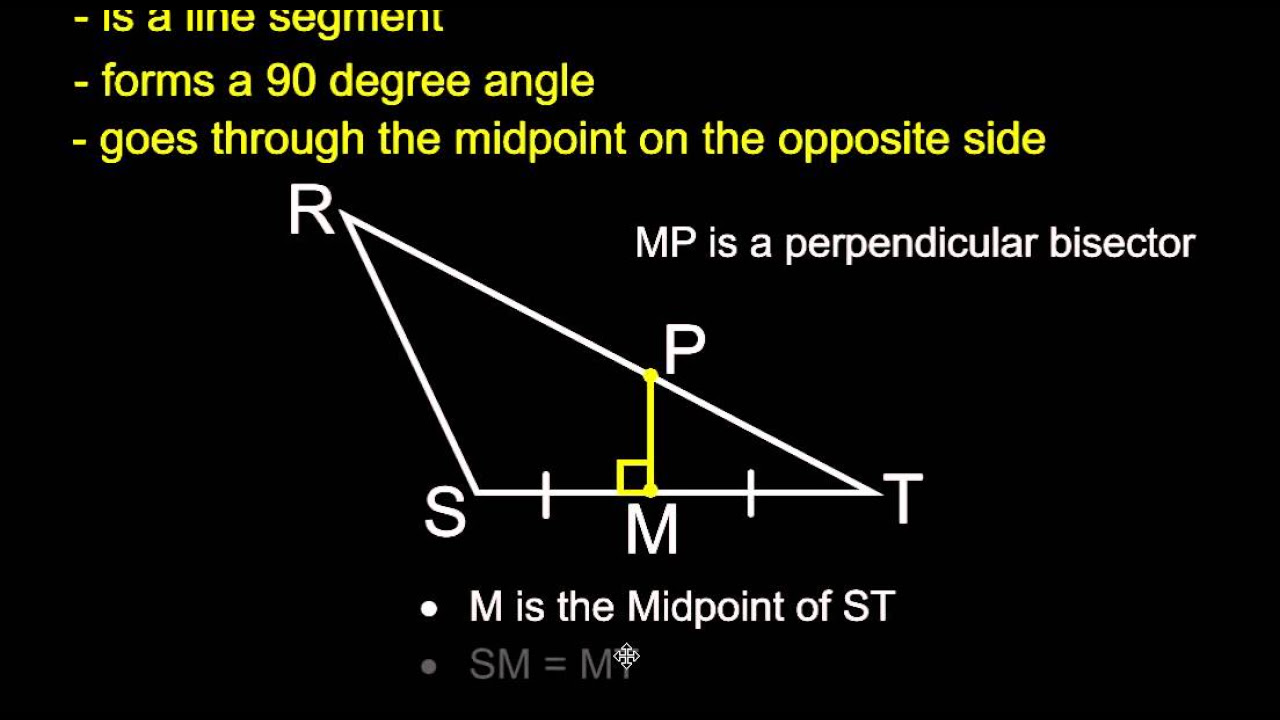
- 🔄 The perpendicular bisector is a line that divides a side into two equal lengths and is perpendicular to that side.
- 🔵 The incenter and circumcenter are related to the inscribed and circumscribed circles, respectively, with the incenter being the center of the inscribed circle and the circumcenter being the center of the circumscribed circle.
- 📘 The script provides a comprehensive review of identifying the incenter, centroid, orthocenter, and circumcenter of a triangle.
Q & A
What is the incenter of a triangle?
-The incenter of a triangle is the point where the three angle bisectors of the triangle intersect. It is always located inside the triangle and is the center of the inscribed circle (incircle) of the triangle.
How do you find the centroid of a triangle?
-The centroid of a triangle is found by the intersection of the three medians of the triangle. A median is a line segment from a vertex to the midpoint of the opposite side.
What is the relationship between the segments AP and PE in terms of the centroid?
-For the centroid, the segment AP is two-thirds the length of the median AE, and PE is one-third the length of AE. In other words, AP is twice the length of PE.
Can the orthocenter of a triangle always be found inside the triangle?
-No, the orthocenter of a triangle does not always lie inside the triangle. It can be inside an acute triangle, on the right triangle if it's a right triangle, or outside the triangle if it's an obtuse triangle.
How is the orthocenter of a triangle located?
-The orthocenter is located at the intersection of the three altitudes of the triangle. An altitude is a perpendicular line from a vertex to the opposite side.
What is the circumcenter of a triangle?
-The circumcenter of a triangle is the point where the three perpendicular bisectors of the sides of the triangle intersect. It is the center of the circumscribed circle (circumcircle) around the triangle.
Is the circumcenter always inside the triangle?
-No, the circumcenter's location depends on the type of triangle. It is inside an acute triangle, on the right triangle if it's a right triangle, and outside an obtuse triangle.
What is the difference between an incenter and a circumcenter?
-The incenter is the center of the inscribed circle inside the triangle, found by the intersection of the angle bisectors. The circumcenter is the center of the circumscribed circle around the triangle, found by the intersection of the perpendicular bisectors of the sides.
How does the location of the orthocenter differ in a right triangle compared to an obtuse triangle?
-In a right triangle, the orthocenter is located at the right angle vertex, while in an obtuse triangle, the orthocenter lies outside the triangle.
Can you identify the circumcenter of a right triangle by its position on the hypotenuse?
-Yes, the circumcenter of a right triangle is located at the midpoint of the hypotenuse.
What property do the perpendicular bisectors have in relation to the circumcenter?
-The perpendicular bisectors of the sides of a triangle are the lines that are both perpendicular to a side and bisect it, thus creating two congruent segments. The circumcenter is the point where all three of these bisectors intersect.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)