Toán lớp 7 Bài 6 Tính chất ba đường trung trực của tam giác | trang 71, 72 | Chương 8 | Tập 2 | CTST

Summary

This educational video focuses on the properties of perpendicular bisectors in a triangle. The teacher demonstrates how to construct perpendicular bisectors using a ruler and compass, showing how they intersect at a single point. Key concepts covered include the definition of perpendicular bisectors, their relationship to the triangle’s vertices, and their geometric properties. The lesson also explores real-world applications such as finding points equidistant from three fixed points, such as determining the location for a school on a map. Through practice exercises, students learn to apply these principles to both general and right-angled triangles.

Takeaways

• 😀 The lesson introduces the concept of perpendicular bisectors in triangles, focusing on how they relate to the geometry of the triangle.
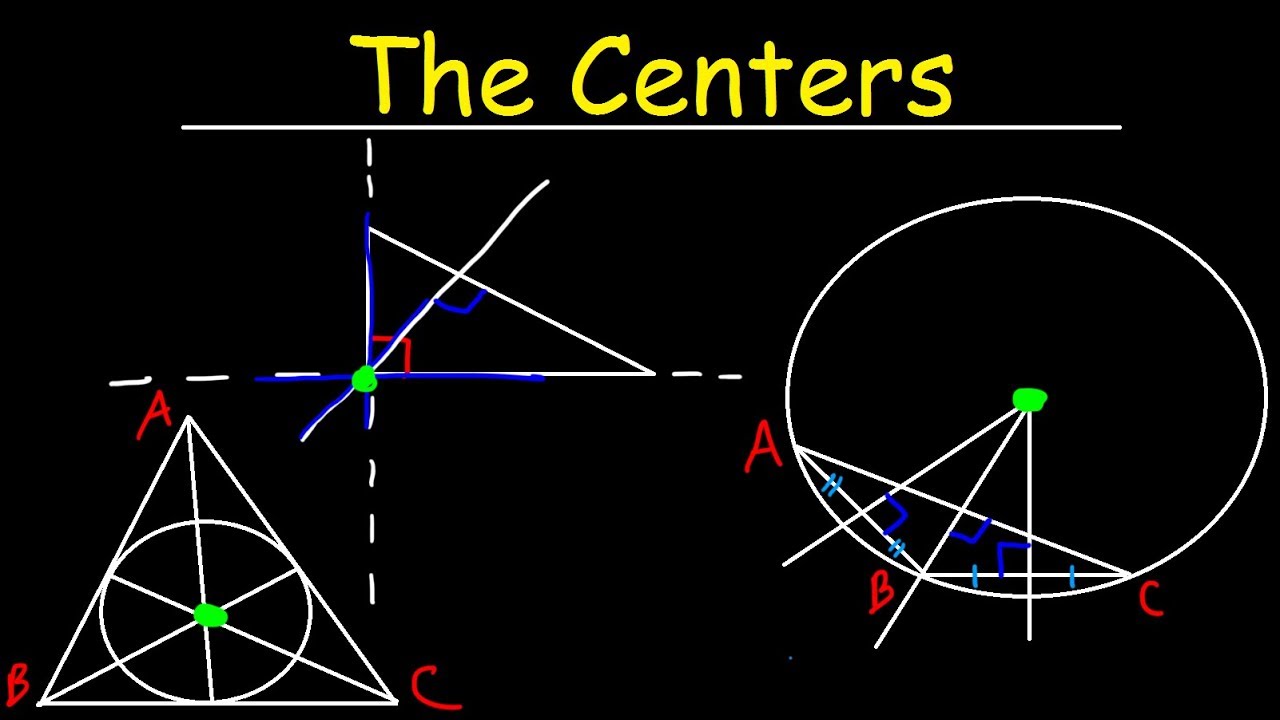
• 😀 Students learn that the perpendicular bisector of each side of a triangle intersects at a single point, called the circumcenter, which is equidistant from all three vertices of the triangle.
• 😀 The script explains how to construct the perpendicular bisectors of a triangle using a ruler and compass, demonstrating how to find the circumcenter.
• 😀 The key property of the perpendicular bisectors in any triangle is that they all meet at a single point, which is equidistant from the triangle's three vertices.
• 😀 The lesson emphasizes that this point of intersection is the center of the circumcircle, which passes through all three vertices of the triangle.
• 😀 In an acute triangle, the three perpendicular bisectors meet inside the triangle, while in a right triangle, they meet at the vertex of the right angle.
• 😀 The activity involving constructing perpendicular bisectors helps students practice drawing and understanding how these bisectors intersect.
• 😀 A practical example involves using the perpendicular bisectors to determine a location that is equidistant from three given points, such as in urban planning or construction projects.
• 😀 The lesson includes a challenge where students need to prove that a point equidistant from all three vertices of a triangle lies on the perpendicular bisectors.
• 😀 A key takeaway from the lesson is that the perpendicular bisectors of any triangle always meet at a point that is equidistant from all three vertices, which has important applications in geometry and real-life situations.

Q & A

What is the main topic discussed in the video script?

The main topic discussed is the perpendicular bisectors of a triangle, including their construction and properties.

What is the definition of a perpendicular bisector in the context of the script?

A perpendicular bisector is a line that divides a segment into two equal parts at a right angle.

How do you construct the perpendicular bisector of a side of a triangle using a compass and ruler?

To construct the perpendicular bisector of a side of a triangle, you draw two arcs with the compass from each endpoint of the side, ensuring the arcs intersect. Then, draw a straight line through the intersection points, which will be the perpendicular bisector.

What is the significance of the point where the three perpendicular bisectors of a triangle meet?

The point where the three perpendicular bisectors meet is called the circumcenter, and it is equidistant from all three vertices of the triangle.

In the script, how is it demonstrated that the perpendicular bisectors intersect at a single point?

It is demonstrated by constructing the perpendicular bisectors of the sides of a triangle and observing that they intersect at a single point, the circumcenter, in both general and specific triangle cases.

What is the geometric property of the circumcenter as mentioned in the script?

The circumcenter is equidistant from all three vertices of the triangle.

What is the key difference between the perpendicular bisectors of a general triangle and a right-angled triangle as discussed in the video?

In both general and right-angled triangles, the perpendicular bisectors intersect at a single point, but in a right-angled triangle, the circumcenter lies on the hypotenuse, whereas, in other triangles, it lies inside or outside depending on the type of triangle.

How can the perpendicular bisectors of a triangle be used in real-world applications, according to the script?

The perpendicular bisectors can be used to determine a point equidistant from three locations, such as finding a site for a school that is equidistant from three residential areas, as shown in the real-world example provided in the video.

What is the relationship between the circumcenter and the circumcircle of a triangle?

The circumcenter is the center of the circumcircle, which is the circle that passes through all three vertices of the triangle.

What can be inferred about the location of the circumcenter in different types of triangles?

In an acute triangle, the circumcenter is inside the triangle, in a right triangle, it lies on the hypotenuse, and in an obtuse triangle, it is outside the triangle.