Resolver una Suma de Riemann paso a paso. #MateYisus

Summary

En este nuevo video, Jesús Grajeda enseña a aproximar una integral utilizando sumas de Riemann. Se presenta un ejercicio específico con una función f(x) = x cúbica - 6x, evaluando la integral en el intervalo [0, 3] con 6 puntos de muestra. Jesús explica el concepto de suma de Riemann y cómo calcular el delta x, evaluando la función en cada punto y sumando los resultados multiplicados por delta x para obtener una aproximación de la integral. Además, se discute cómo la carga de los rectángulos (por la izquierda o derecha) afecta la aproximación y se invita a los espectadores a explorar más sobre el tema en otros videos.

Takeaways

• 😀 Jesús Grajeda enseña cómo aproximar una integral usando sumas de Riemann en este vídeo.
• 📐 El ejercicio práctico consiste en evaluar la suma de Riemann para la función \( f(x) = x^3 - 6x \) en el intervalo [0, 3] utilizando 6 subintervalos.
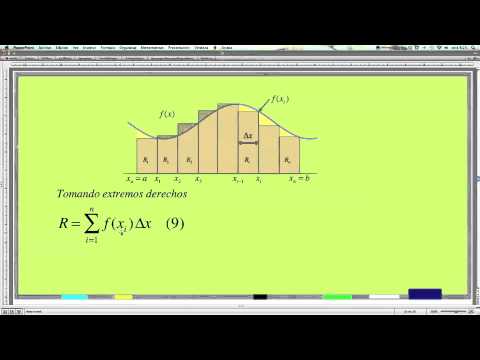
• 📝 Se define la integral como el límite de la suma de Riemann cuando el número de subintervalos \( n \) tiende a infinito.
• 🔢 Se calcula \( \Delta x \) como \( \frac{b-a}{n} \), donde \( a = 0 \), \( b = 3 \), y \( n = 6 \), resultando en \( \Delta x = 0.5 \).
• 📊 Se evalúa la función \( f(x) \) en los puntos \( x_i \) que se encuentran cada \( \Delta x \) a lo largo del intervalo.
• 📈 Se calculan los valores de \( f(x) \) en los puntos \( x_i \) y se multiplican por \( \Delta x \) para obtener la suma de Riemann.
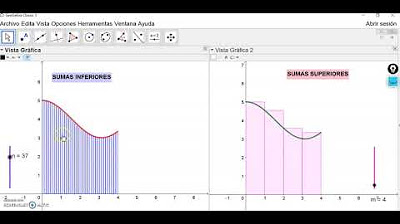
• 🧮 Se obtiene un resultado aproximado de la integral, que en este caso es negativo debido a que la función está por debajo del eje x en el intervalo considerado.
• 📉 La gráfica muestra que los rectángulos se cargan hacia el lado derecho de cada \( x_i \) para aproximar el área bajo la curva.
• 🔄 Se discute cómo el resultado de la suma de Riemann varía si se carga hacia el lado izquierdo o derecho, y se enfatiza la importancia de \( n \) tender a infinito para obtener una aproximación exacta.
• 🎓 Se invita a los espectadores a explorar más sobre la notación sigma y la aproximación de áreas bajo curvas con sumas de Riemann en otros videos.

Q & A

¿Qué es la suma de Riemann y cómo se utiliza para aproximar una integral?

La suma de Riemann es una aproximación de una integral definida, que se calcula como el límite cuando n tiende a infinito de la suma de los productos de la función evaluada en puntos del intervalo dividido y el ancho de dicho intervalo dividido entre n.

¿Cuál es la función que se está aproximando en el script proporcionado?

La función que se está aproximando es f(x) = x cúbica - 6x.

¿Cuáles son los puntos extremos y el número de divisiones utilizadas para la aproximación en el script?

Los puntos extremos son a = 0 y b = 3, y se utiliza un total de n = 6 divisiones para la aproximación.

¿Cómo se define el ancho del intervalo (delta x) para la aproximación en la suma de Riemann?

El ancho del intervalo (delta x) se define como (b - a) / n, donde b y a son los puntos extremos y n es el número de divisiones.

¿Cómo se eligen los puntos de evaluación dentro del intervalo para la suma de Riemann?

Los puntos de evaluación se eligen de tal forma que cada uno esté a un delta x distancia del siguiente, y se evalúa la función en estos puntos.

¿Qué significa el resultado negativo que se obtiene en la aproximación y cómo se interpreta gráficamente?

El resultado negativo indica que la aproximación incluye áreas bajo la curva que están por debajo del eje x, lo cual se interpreta como áreas negativas en el gráfico.

¿Cómo se cargan los rectángulos en la aproximación y cómo afecta esto al resultado?

Los rectángulos se cargan hacia el lado derecho de cada punto de evaluación (x_i). Si se cargaran hacia el lado izquierdo, el valor aproximado del integral cambiaría, ya que se estaría considerando una aproximación diferente de la área bajo la curva.

¿Por qué es importante la elección de n cuando se utiliza la suma de Riemann para aproximar una integral?

La elección de n es importante porque cuanto mayor sea n, más preciso será el resultado de la aproximación, ya que se utilizarán más rectángulos para estimar la área bajo la curva.

¿Qué es la notación sigma y cómo se relaciona con la suma de Riemann?

La notación sigma representa la sumatoria en matemáticas, y se utiliza en la suma de Riemann para indicar la suma de los productos de la función evaluada en puntos del intervalo y el ancho del intervalo.

¿Cómo se puede mejorar la aproximación de la integral utilizando la suma de Riemann?

La aproximación de la integral se puede mejorar aumentando el número de divisiones (n), utilizando métodos de integración más avanzados, o evaluando la función en puntos más adecuados dentro del intervalo.