TRANSFORMADA Z - Parte 1: Definición (REVISAR DESCRIPCIÓN) | El Traductor
Summary
TLDREn este video, el ponente explica la transformada Z y su relación con la transformada de Laplace. A diferencia de la transformada de Laplace, que se aplica a señales continuas, la transformada Z se utiliza para secuencias discretas, con la variable compleja `z`. Se detalla cómo calcular la transformada Z mediante una suma infinita, similar al cálculo de la transformada de Laplace mediante una integral impropia. Además, se menciona la importancia de la convergencia de la serie para obtener un resultado válido y cómo la transformada Z se puede simplificar a una serie geométrica en algunos casos.
Takeaways
- 😀 Se explica que la transformada Z es muy útil para resolver sistemas concretos y señales discretas.
- 😀 La transformada Z es análoga a la transformada de Laplace, pero se aplica a secuencias con variables discretas.
- 😀 A diferencia de la transformada de Laplace, que usa variables complejas continuas, la transformada Z utiliza una variable compleja de secuencias discretas.
- 😀 La transformada Z se define mediante una suma infinita, similar a la integral de la transformada de Laplace, pero con un enfoque de sumatoria.
- 😀 Es importante entender que la transformada Z se aplica a señales de variables independientes discretas, representadas por secuencias como x[n].
- 😀 La transformada Z se calcula mediante una serie sumatoria, lo que requiere encontrar a qué valor converge dicha serie.
- 😀 La fórmula general para calcular la transformada Z implica sumar términos en una secuencia, evaluando la función en cada término de la secuencia.
- 😀 La región de convergencia de la transformada Z es esencial para que esta sea válida, de forma similar a cómo ocurre en la transformada de Laplace.
- 😀 La transformada Z se utiliza principalmente para analizar señales discretas y estudiar sus características dentro de un dominio complejo.
- 😀 La mayoría de las veces, se pueden calcular las transformadas Z utilizando patrones geométricos, lo que facilita el proceso de resolución.
Q & A
¿Qué es la transformada Z y en qué se diferencia de la transformada de Laplace?
-La transformada Z es una herramienta utilizada para analizar señales discretas en el dominio complejo, similar a la transformada de Laplace, pero mientras la Laplace se aplica a señales continuas, la Z se aplica a secuencias discretas. Ambas transformadas tienen una variable compleja, pero la Z trabaja con sumatorias en lugar de integrales.
¿Cuál es la principal diferencia entre señales continuas y discretas en términos de transformadas?
-Las señales continuas se representan en términos de una variable continua, mientras que las señales discretas se representan en términos de valores de la variable independiente en puntos específicos (números enteros). La transformada Z se utiliza para señales discretas, mientras que la transformada de Laplace se aplica a señales continuas.
¿Qué significa la 'región de convergencia' en la transformada Z?
-La región de convergencia (ROC) es el conjunto de valores de la variable compleja 'z' para los cuales la sumatoria de la transformada Z converge, es decir, para los cuales la transformada Z es válida y no diverge.
¿Cómo se calcula la transformada Z de una secuencia discreta?
-La transformada Z se calcula sumando los términos de la secuencia multiplicados por potencias negativas de la variable compleja z. El proceso general es: X(z) = Σ x[n] z^(-n), donde x[n] es el valor de la secuencia en el tiempo n.
¿Qué significa que la transformada Z sea análoga a la transformada de Laplace?
-La analogía se refiere a que ambas transformadas transforman señales en el dominio del tiempo (ya sea continuo o discreto) a un dominio complejo, permitiendo analizar las señales en términos de sus componentes en el dominio complejo. La principal diferencia radica en que Laplace es para señales continuas y Z es para señales discretas.
¿Qué rol juega la variable 'z' en la transformada Z?
-La variable 'z' en la transformada Z es una variable compleja que permite representar las secuencias discretas en el dominio complejo. A través de z, se puede analizar la estabilidad y el comportamiento de las secuencias de señales.
¿Cómo se puede simplificar la transformada Z en algunos casos?
-En muchos casos, la transformada Z puede simplificarse utilizando propiedades de series geométricas, lo que facilita los cálculos. Esto permite identificar patrones o comportamientos en las secuencias y obtener una solución más directa.
¿Qué quiere decir que la transformada Z se utiliza para 'resolver cualquier transformada Z'?
-Esto significa que la transformada Z es una herramienta general que puede aplicarse para encontrar la representación en el dominio complejo de cualquier secuencia discreta, permitiendo analizar su comportamiento, estabilidad y otras propiedades relevantes.
¿Por qué se menciona que la transformada Z 'se calcula mirando la secuencia como una serie geométrica'?
-Se menciona porque muchas secuencias discretas tienen una estructura similar a una serie geométrica, lo que permite usar las propiedades de las series geométricas para simplificar la evaluación de la transformada Z, haciendo los cálculos más fáciles de manejar.
¿Qué importancia tiene la 'sumatoria infinita' en el cálculo de la transformada Z?
-La sumatoria infinita es crucial porque refleja la acumulación de todos los términos de la secuencia en el dominio complejo. Para que la transformada Z sea válida, esta sumatoria debe converger, lo que implica que solo ciertos valores de la variable z garantizarán la existencia de la transformada.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Transformada de Laplace #1 | Desde cero

INTRODUCCION A LA TRANSFORMADA Z | 25/51 | UPV

Laplace con matlab. Vídeo 5
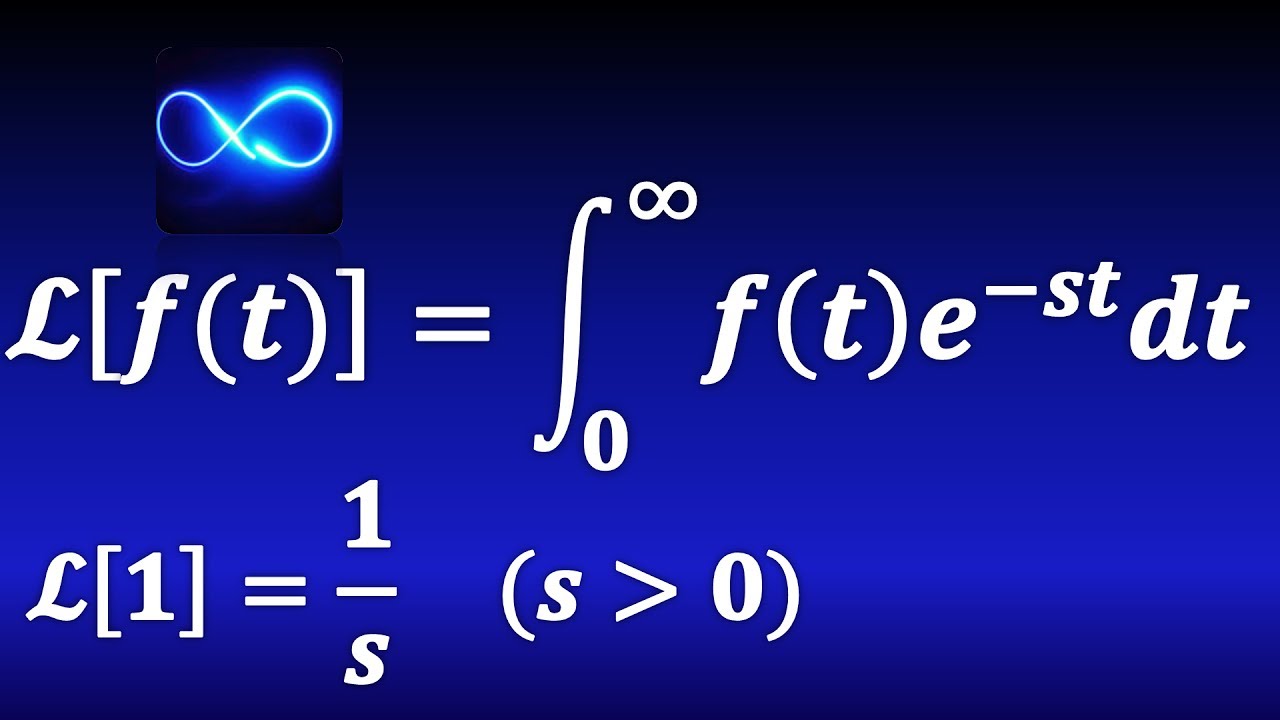
168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.

170. Transformada de Laplace: Propiedades de linealidad, con demostraciones y ejemplos

CIRCUITO RL SERIE - LUCIO ELÉCTRICO
5.0 / 5 (0 votes)
