Transformada de Laplace #1 | Desde cero
Summary
TLDREn este primer video de la serie sobre transformadas de Laplace, el canal de física y matemáticas explica cómo calcular la transformada de Laplace de una función. La presentadora enseña el proceso de pasar de una función 'f(t)' a su transformada 'F(s)', destacando la importancia de esta herramienta en problemas de física y matemáticas. Se presenta una tabla de integrales tabuladas para facilitar el cálculo de transformadas de funciones comunes, y se ejemplifica con la transformada de funciones como 't^n' y 'sen(8t)'. Además, se introducen propiedades como el producto por una constante y la linealidad, con ejercicios prácticos para ilustrar su aplicación. El video invita a la suscripción y participación activa, prometiendo más contenido en futuras entregas.
Takeaways
- 😀 La transformada de Laplace es una herramienta matemática utilizada para analizar funciones, particularmente en el ámbito de la física y las matemáticas aplicadas.
- 📚 Se presenta una serie de videos sobre la transformada de Laplace, comenzando con la explicación de cómo calcularla para una función dada.
- 🔍 La función de ejemplo en el script es \( e^{t} \), donde \(t\) es un número real mayor que 0, y se busca calcular su transformada de Laplace, que depende de una variable \( s \).
- 📉 La transformada de Laplace convierte una función del dominio de tiempo (\( f(t) \)) en una función del dominio de frecuencia compleja (\( F(s) \)).
- 🛠️ Existe un proceso inverso a la transformada de Laplace, conocido como la transformada inversa de Laplace, que permite recuperar la función original a partir de su transformada.
- 📝 La transformada de Laplace se define matemáticamente como una integral desde 0 hasta el infinito de \( e^{-st} \cdot f(t) \), donde \( s \) es una variable compleja.
- 📋 Las integrales para calcular la transformada de Laplace de funciones comunes están tabuladas y disponibles en una tabla para facilitar su uso sin necesidad de calcularlas manualmente.
- 🔢 Se ilustra cómo utilizar la tabla de transformadas de Laplace para encontrar la transformada de funciones simples, como \( t^n \), donde \( n \) es un número natural.
- 🆚 Se mencionan propiedades de la transformada de Laplace, como el producto por una constante y la propiedad de linealidad, que simplifican el cálculo de transformadas de funciones más complejas.
- 📚 Se animará a los espectadores a suscribirse al canal y a dejar comentarios con sugerencias y dudas para futuras sesiones de aprendizaje.
- 👋 El script concluye con un saludo y una promesa de continuar la serie de videos en futuras oportunidades.
Q & A
¿Qué es la transformada de Laplace y cómo se relaciona con la función original?
-La transformada de Laplace es una técnica matemática que convierte una función de tiempo en otra función que depende de una variable compleja, generalmente denotada como 's'. Es útil porque en muchos problemas es más cómoda trabajar con la transformada que con la función original.
¿Cuál es el proceso de calcular la transformada de Laplace de una función?
-El proceso de calcular la transformada de Laplace de una función 'f(t)' consiste en integrar la función multiplicada por un factor exponencial decreciente 'e^(-st)' desde 0 hasta el infinito.
¿Por qué es importante mantener la anotación estándar al referirse a la transformada de Laplace de una función?
-La anotación estándar es importante para diferenciar claramente entre la función original 'f(t)' y su transformada 'F(s)', lo que evita confusiones y facilita la comunicación en el análisis de sistemas.
¿Qué es la tabla de transformadas de Laplace y cómo se utiliza?
-La tabla de transformadas de Laplace es una herramienta que lista funciones comunes junto con sus correspondientes transformadas de Laplace. Se utiliza para encontrar rápidamente la transformada de una función sin tener que calcular la integral directamente.
¿Cómo se calcula la transformada de Laplace de una función elevada a un número natural 'n'?
-Para calcular la transformada de Laplace de una función 't^n' donde 'n' es un número natural, se utiliza la fórmula 'n! / (s^(n+1))', donde 'n!' es el factorial de 'n' y 's' es la variable de la transformada.
¿Qué propiedad se utiliza para calcular la transformada de Laplace de un producto de una constante y una función?
-Se utiliza la propiedad del producto por una constante, la cual indica que la transformada de Laplace de una constante multiplicada por una función es igual a la constante multiplicada por la transformada de Laplace de la función.
¿Cómo se calcula la transformada de Laplace de un seno de 'at', donde 'a' es una constante?
-La transformada de Laplace del seno de 'at' es 'a / (s^2 + a^2)', donde 's' es la variable de la transformada y 'a' es la constante de la función seno.
¿Qué es la propiedad de linealidad en el contexto de las transformadas de Laplace?
-La propiedad de linealidad establece que la transformada de Laplace de una suma o resta de funciones es igual a la suma o resta de las transformadas de Laplace de cada función individual, multiplicadas por sus correspondientes constantes.
¿Cómo se calcula la transformada de Laplace de una función que es una combinación lineal de otras funciones?
-Para calcular la transformada de Laplace de una función que es una combinación lineal de otras, se aplica la propiedad de linealidad, sumando o restando las transformadas de Laplace de cada término, multiplicadas por sus respectivas constantes.
¿Qué se aprenderá en los siguientes videos de la serie sobre transformadas de Laplace?
-En los siguientes videos de la serie, se explorarán más propiedades de las transformadas de Laplace y se realizarán ejemplos prácticos para ilustrar cómo resolver problemas utilizando estas propiedades.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

170. Transformada de Laplace: Propiedades de linealidad, con demostraciones y ejemplos

Laplace con matlab. Vídeo 5

TRANSFORMADA Z - Parte 1: Definición (REVISAR DESCRIPCIÓN) | El Traductor

171. Laplace Transform hyperbolic sine, using definition of sinh

CIRCUITO RL SERIE - LUCIO ELÉCTRICO
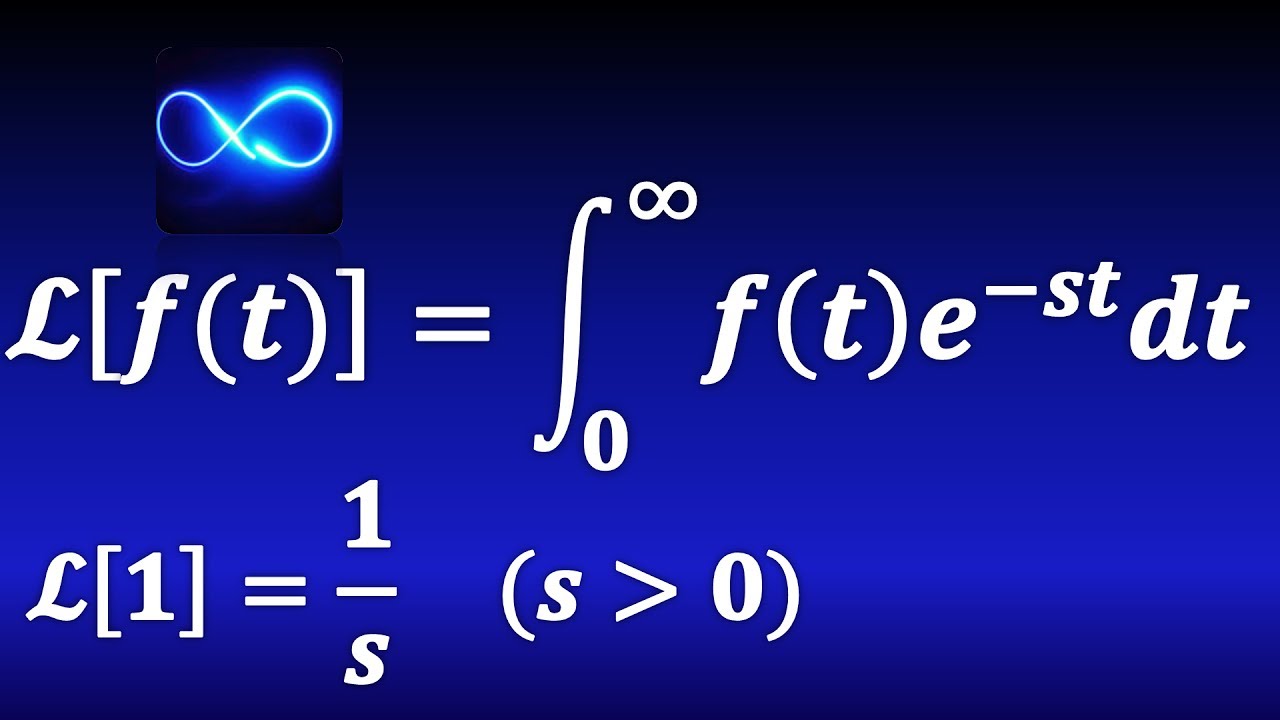
168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.
5.0 / 5 (0 votes)
