170. Transformada de Laplace: Propiedades de linealidad, con demostraciones y ejemplos
Summary
TLDREn este video, se explican propiedades clave de las transformadas de Laplace, como la linealidad, que establece que la transformada de una constante multiplicada por una función es igual a la constante multiplicada por la transformada de la función. Además, se aborda cómo sumar y restar funciones dentro de la transformada, dividiendo el cálculo en transformadas individuales. Se dan ejemplos prácticos, como la transformada de la constante 5, y se explica cómo calcular la transformada de expresiones más complejas. El video también invita a los espectadores a calcular la transformada del seno hiperbólico y ofrece un procedimiento completo en el siguiente video.
Takeaways
- 😀 La transformada de Laplace es lineal y tiene propiedades que permiten simplificar cálculos.
- 😀 Una de las propiedades de linealidad es que la transformada de Laplace de una constante por una función es igual a la constante multiplicada por la transformada de la función.
- 😀 La demostración de esta propiedad se realiza utilizando la definición de la transformada de Laplace y las propiedades de las integrales.
- 😀 Para calcular la transformada de Laplace de una constante multiplicada por una función, se puede sacar la constante de la integral.
- 😀 La transformada de Laplace de un número constante, como 5, es simplemente 5 dividido entre 's'.
- 😀 Otra propiedad importante es la de la suma o resta de funciones: la transformada de Laplace de una suma o resta de funciones es igual a la suma o resta de sus transformadas de Laplace.
- 😀 Esta propiedad se puede demostrar a partir de la definición de la transformada de Laplace, usando la propiedad de las integrales.
- 😀 Al separar la integral en dos partes (cuando se suma o resta), se deben considerar los casos en los que las integrales pueden diverger.
- 😀 Al aplicar estas propiedades de linealidad, se pueden calcular transformadas de Laplace más complejas sin necesidad de usar la definición directamente.
- 😀 Un ejemplo práctico es el cálculo de la transformada de Laplace de una expresión como 5 - e^(2t) + 3e^t, usando las propiedades ya demostradas.
- 😀 Finalmente, la transformada de Laplace del seno hiperbólico puede calcularse utilizando las propiedades vistas en el video, y se promete que el procedimiento completo será explicado en el siguiente video.
Q & A
¿Qué propiedad de las transformadas de Laplace se menciona al principio del video?
-La propiedad mencionada es la linealidad de la transformada de Laplace, que establece que la transformada de Laplace de una constante multiplicada por una función es igual a la constante multiplicada por la transformada de Laplace de la función.
¿Cómo se demuestra la propiedad de linealidad de la transformada de Laplace?
-La propiedad se demuestra a partir de la definición de la transformada de Laplace, utilizando la integral y aplicando una propiedad de las integrales que permite sacar la constante fuera de la integral.
¿Qué ocurre cuando se calcula la transformada de Laplace de una constante como 5?
-Se puede calcular la transformada de Laplace de la constante 5 de manera simple, reconociendo que 5 * 1 es una función constante, y aplicando la propiedad de linealidad. La transformada de Laplace de 1 es 1/s, por lo que la transformada de 5 será 5/s.
¿Qué sucede cuando sumamos o restamos funciones al calcular la transformada de Laplace?
-La propiedad de suma o resta establece que la transformada de Laplace de una suma o resta de funciones es igual a la suma o resta de las transformadas de Laplace de las funciones individuales.
¿Cómo se demuestra la propiedad de la suma o resta de funciones en las transformadas de Laplace?
-Se demuestra mediante la definición de la transformada de Laplace, separando la integral en dos partes, una para cada función. Sin embargo, se debe tener cuidado con la convergencia de las integrales impropias.
¿Qué precaución se debe tomar al aplicar la propiedad de la suma o resta en integrales impropias?
-Se debe tener cuidado porque, aunque una integral pueda converger, las otras podrían diverger. Es importante verificar que tanto las funciones involucradas tengan una transformada de Laplace definida.
¿Cómo se aplica la propiedad de linealidad al calcular la transformada de Laplace de una expresión como 5 - e^(2t) + 3e^t?
-Se aplica la propiedad de linealidad separando la transformada de cada término: 5 se transforma como 5/s, e^(2t) se transforma como 1/(s-2), y 3e^t se transforma como 3/(s-1). Luego se combinan los resultados.
¿Qué fórmula se utiliza para calcular la transformada de Laplace de una función como e^(at)?
-La fórmula utilizada para calcular la transformada de Laplace de e^(at) es 1/(s - a), donde 'a' es el exponente de la función exponencial.
¿Cómo se calcula la transformada de Laplace de funciones que incluyen constantes multiplicadas?
-Si una constante multiplica una función, la constante se puede sacar de la transformada de Laplace, lo que facilita el cálculo. Por ejemplo, para 3e^t, se multiplica la transformada de e^t por 3.
¿Qué es el seno hiperbólico y cómo se relaciona con la transformada de Laplace?
-El seno hiperbólico de x, definido como (e^x - e^(-x))/2, es una función que aparece frecuentemente en cálculos de transformadas de Laplace. El video invita a calcular la transformada de Laplace del seno hiperbólico de at en un video posterior.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Transformada de Laplace #1 | Desde cero
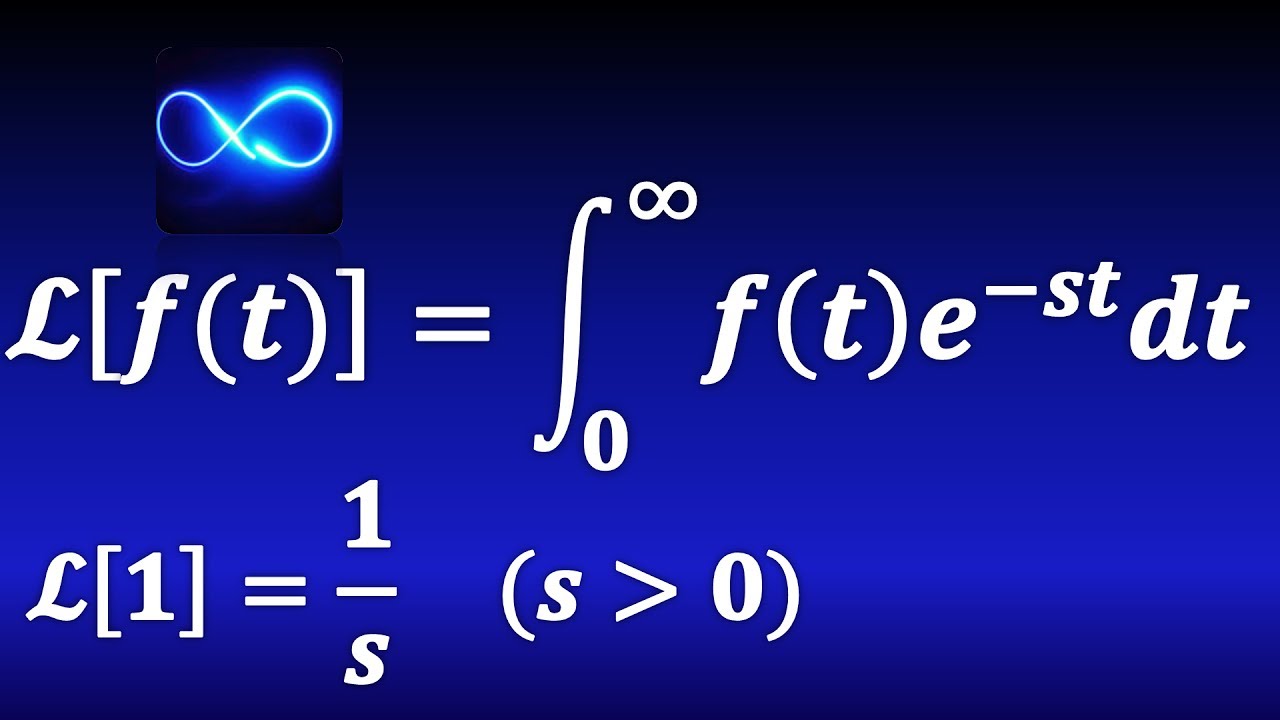
168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.

DERIVADA DE UNA CONSTANTE DIVIDIDA POR UNA FUNCIÓN

Teoremas de derivación. Reglas básicas para derivadas. Cálculo diferencial

Derivadas de Funciones Algebraicas | Video 3

Reglas para integrar una función. Teoremas básicos para integrales o antiderivadas de funciones.
5.0 / 5 (0 votes)
