4 3 Interest points
Summary
TLDRThe video explains the concept of interest points in image processing, focusing on how specific points, like corners or intersections of edges, are crucial for robust detection. It highlights the role of image gradients in identifying interest points and introduces Moravec's corner detection method, which uses the sum of squared differences to measure changes in pixel patches. However, Moravec's method struggles with slanted edges, leading to incorrect corner identification. The video sets up this problem and suggests upcoming solutions to improve the robustness of detecting interest points in images.
Takeaways
- 🔍 Interest points are well-defined locations in an image that can be detected robustly.
- 📐 A point within a uniform area is not an interest point because its position is not well-defined.
- 🟦 Corners or intersections of two edges are typical interest points as they can be detected even when the camera moves.
- 📈 An interest point can also be defined as a position where the image gradient has significant values in both the x and y directions.
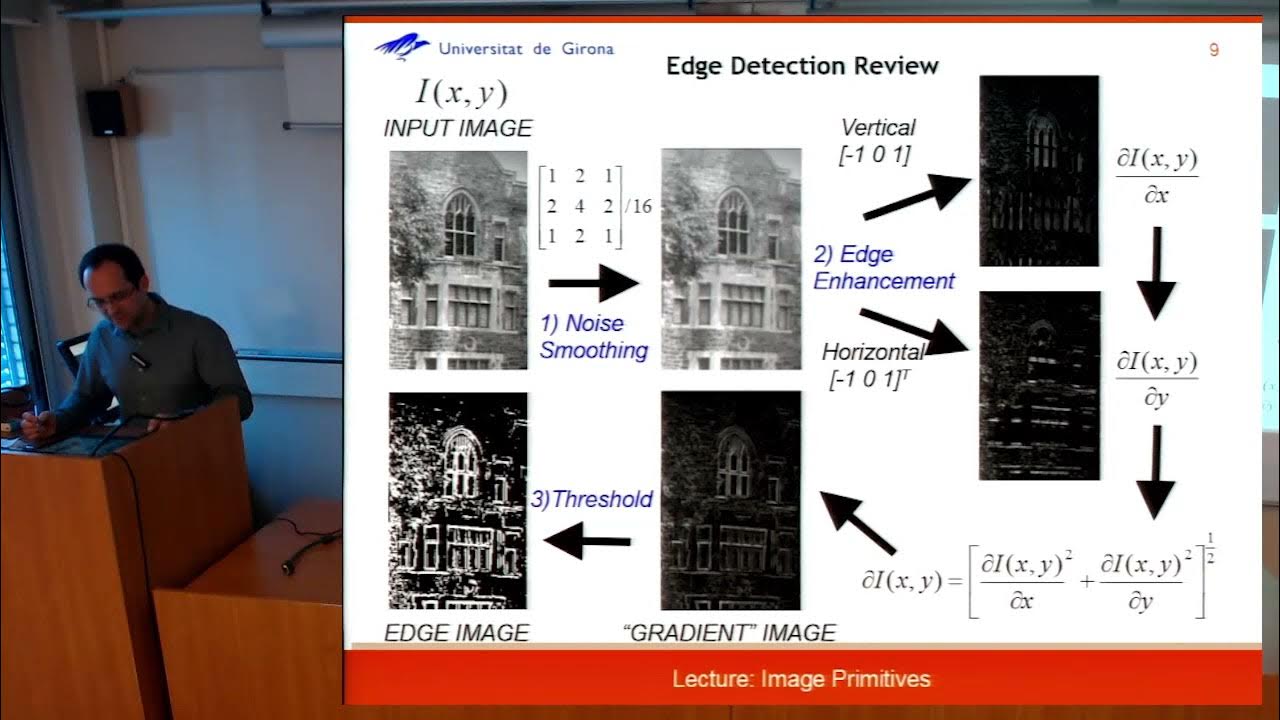
- 🧮 The gradient image, not the binary edge image, is key to detecting corners since it captures more detail.
- 🧠 Moravic’s corner detector defines a corner as a point with low self-similarity, which is determined by comparing shifted patches.
- 🔄 Shifting a window around a point and comparing patches in different directions allows for identifying interest points.
- 💡 The sum of square differences is used to compare patches, helping to avoid positive and negative differences canceling out.
- ⚠️ Moravic's detector struggles with slanted edges, incorrectly classifying them as corners.
- 🔧 The limitations of Moravic's detector highlight the need for more advanced methods to handle certain types of edges and points.
Q & A
What is an interest point in an image?
-An interest point is a point in an image that has a well-defined location and can be detected robustly. It often corresponds to distinctive features like corners or intersections of edges, making it easy to detect even if the image is slightly shifted.
Why is the middle of a square not considered an interest point?
-The middle of a square is not considered an interest point because its location is not well-defined. If the camera moves slightly, it would be difficult to detect the same point again, unlike more distinct features such as corners.
What makes a corner a good candidate for an interest point?
-A corner is a good interest point because it has a well-defined position. Even if the camera shifts slightly, the corner remains easily detectable due to its sharp changes in the gradient along different directions.
How are interest points related to image gradients?
-Interest points are often identified in regions where the image gradient is significant in both the x and y directions. The gradient represents changes in intensity, and high values in both directions suggest a feature, such as a corner, that can be robustly detected.
What is the Moravic corner detector?
-The Moravic corner detector is one of the first corner detection algorithms. It identifies a corner by measuring self-similarity—if a point has low self-similarity when the surrounding window is shifted in different directions, it is classified as a corner.
How does the Moravic detector calculate self-similarity?
-The Moravic detector compares patches of pixels by shifting a window around the interest point. It calculates the sum of squared differences between pixel intensities in the original and shifted patches, determining how similar they are.
What is the sum of squared differences (SSD) used for in Moravic's method?
-The sum of squared differences (SSD) is used to quantify how different two patches of an image are. It computes the difference between pixel intensities in the original and shifted patches, squares the differences, and sums them to prevent positive and negative differences from canceling each other out.
Why does the Moravic detector fail with slanted edges?
-The Moravic detector fails with slanted edges because it treats the slanted edge as a corner. This happens because the gradient changes in multiple directions when moving along the edge, even though it’s not a true corner, leading to false detections.
What is the main problem identified in Moravic's method?
-The main problem in Moravic's method is its inability to handle slanted edges. The algorithm incorrectly classifies slanted edges as corners because it detects changes in all directions, which is not always an accurate indicator of a corner.
What is the significance of setting a threshold in the Moravic corner detection method?
-Setting a threshold in the Moravic corner detection method is important for determining whether the changes in pixel intensities are significant enough to classify a point as a corner. If the sum of squared differences exceeds the threshold in all directions, the point is identified as a corner.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)