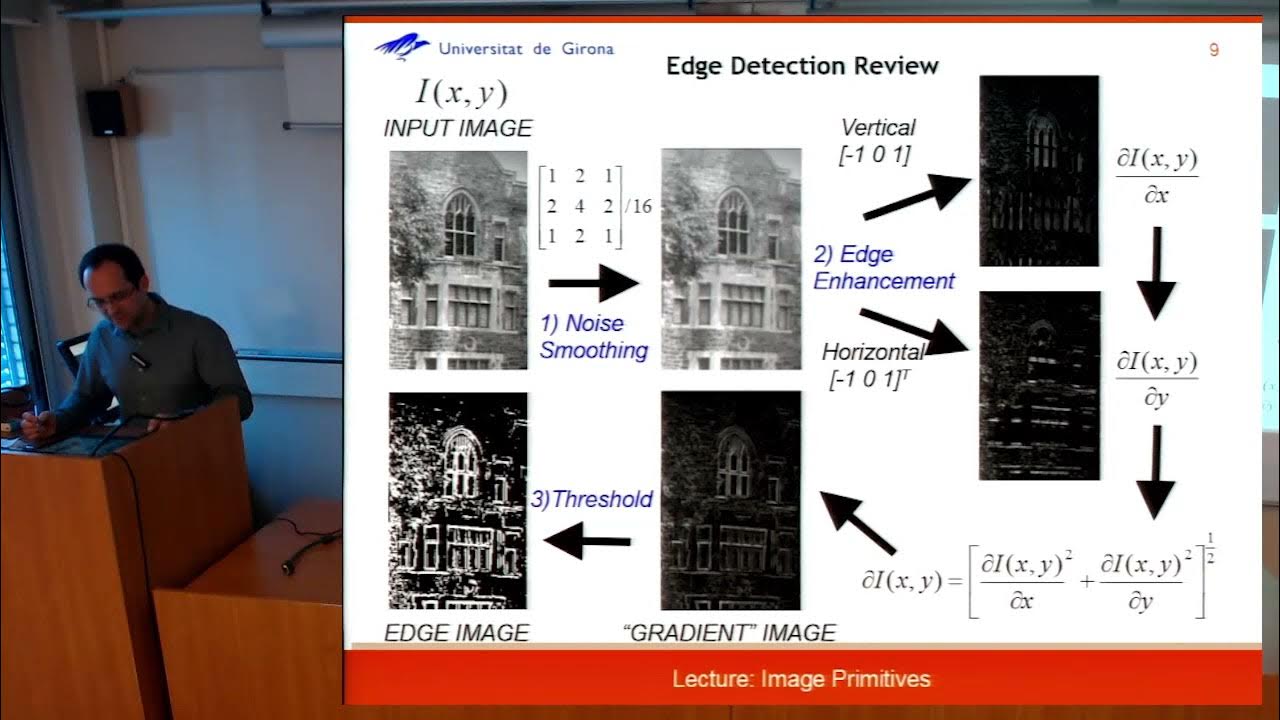
Edge Detection Using Gradients | Edge Detection
Summary
TLDRThis video explains the concept of edge detection in images using the gradient operator, focusing on the first derivative approach. It starts with a simple 1D signal and extends to 2D images, demonstrating how the gradient (composed of partial derivatives with respect to x and y) helps detect edges. The video covers different gradient operators, their trade-offs between localization and noise resilience, and explains how to calculate edge strength and orientation. It concludes with a discussion on thresholding techniques to define edges in an image, paving the way for more advanced edge detection and boundary refinement.
Takeaways
- 😀 Edge detection in images uses the first derivative to identify rapid changes in intensity, which correspond to edges.
- 😀 The gradient operator in 2D images calculates partial derivatives in both x and y directions to detect edges.
- 😀 The gradient magnitude (strength of the edge) is computed as the square root of the sum of squares of the x and y partial derivatives.
- 😀 The gradient orientation gives the direction of the edge using the arctangent of the ratio of the y and x derivatives.
- 😀 For discrete images, finite difference approximations are used to compute derivatives since continuous derivatives don't directly apply.
- 😀 Convolution with specific filters can be used to compute the gradient, with separate filters for the x and y directions.
- 😀 Different gradient operators (e.g., Roberts, Prewitt, Sobel) vary in size, with larger operators providing better noise resilience but poorer edge localization.
- 😀 Smaller gradient operators are more localized but are sensitive to noise, as they only use a small number of pixels for the calculation.
- 😀 Thresholding is used to classify pixels as edges or non-edges, typically by comparing the gradient magnitude to a threshold value.
- 😀 A more advanced form of thresholding, called hysteresis, uses two thresholds to improve edge detection by considering the context of neighboring pixels.
- 😀 The final edge map after thresholding may still contain scattered edges, and further processing is needed to form clean boundaries.
Q & A
What is the purpose of using the gradient operator in edge detection?
-The gradient operator is used in edge detection to identify rapid changes in intensity within an image, which correspond to edges. It works by calculating the first derivative of an image, highlighting areas where the intensity changes quickly.
How does the gradient operator relate to the concept of a 1D edge?
-In a 1D image, an edge is characterized by a rapid change in intensity. The gradient operator computes the first derivative of the image, which reveals the points where the intensity change is highest—these points are the edges.
How can the first derivative of a function be interpreted in the context of edge detection?
-The first derivative of a function represents the rate of change of the function. In edge detection, it indicates where the intensity of an image changes rapidly, which corresponds to the location of edges in the image.
What does the first derivative of a 1D image function look like at the edges?
-At an edge, the first derivative of the 1D image function is 0 on either side of the edge, with a peak at the location of the edge itself. The magnitude of the peak indicates the strength of the edge.
How does the gradient operator extend to 2D images?
-In 2D images, the gradient operator calculates partial derivatives with respect to both the x and y axes. This gives a vector at each pixel, where the x and y components represent the rate of change in each direction, helping to identify the strength and orientation of edges.
What is the difference between the x and y components of the gradient operator?
-The x component of the gradient operator represents the rate of change in the horizontal direction, while the y component represents the rate of change in the vertical direction. These components together indicate the magnitude and orientation of edges in the image.
How do you compute the magnitude and orientation of an edge from the gradient components?
-The magnitude of the edge is computed as the square root of the sum of the squares of the x and y gradient components. The orientation is determined by taking the inverse tangent (atan) of the ratio of the y component to the x component.
Why are finite differences used for computing derivatives in discrete images?
-Finite differences are used because they approximate derivatives in a discrete image. In a continuous image, derivatives are calculated with calculus, but in discrete images, we use differences between neighboring pixel values to estimate the derivative.
What is the advantage of using convolution to implement the gradient operator?
-The gradient operator can be efficiently implemented using convolution with specific filters. This approach allows for fast computation of the gradient at each pixel, making it suitable for image processing tasks.
How does the size of the operator affect edge detection results?
-Smaller operators provide better localization of edges but are more sensitive to noise, as they only consider a small number of neighboring pixels. Larger operators offer better noise resilience by smoothing the image, but they may suffer from poorer localization due to considering a wider range of pixels.
What is the role of thresholding in edge detection, and what are the two common approaches?
-Thresholding is used to decide whether a pixel should be considered part of an edge or not based on its gradient magnitude. The two common approaches are using a single threshold (where pixels with a magnitude above a certain value are considered edges) and hysteresis (which uses two thresholds to allow some context and continuity in edge detection).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
4 2 Filtering
Applying First Principles to x² (1 of 2: Finding the Derivative)

12.2 Finding the derivative (PURE 1- Chapter 12: Differentiation)
Edge detection in digital image processing : Dr. Manjusha Deshmukh
Applying First Principles to x² (2 of 2: What do we discover?)

Detecting Blobs | SIFT Detector
5.0 / 5 (0 votes)