Konvolusi Citra Digital
Summary
TLDRThis video explains the concept of convolution in digital image processing, particularly its role in improving image quality. It discusses how convolution operates by applying a filter (kernel) to the original image, affecting pixels based on their neighboring values. The process is demonstrated step-by-step with an example, highlighting how convolution can be used for various tasks such as noise reduction and edge detection. The speaker also covers different methods for handling image borders during convolution and emphasizes that the choice of kernel influences the output of the operation.
Takeaways
- 🔍 Convolution is a fundamental operation in digital image processing, particularly at the local level, where the value of a pixel is influenced by neighboring pixels.
- 🔄 Convolution uses a kernel, a matrix that is applied to the image, to modify the pixel values and enhance image quality.
- 📏 Kernels are typically smaller than the original image, with common sizes being 3x3, 5x5, or other dimensions.
- 🎯 The origin point of the kernel, usually located at the center of the matrix, determines where the convolution result will be placed in the output image.
- 🔢 Convolution is not simply matrix multiplication; it involves matching positions of kernel values and image pixel intensities and multiplying them together.
- 🖼️ The clipping process is important in convolution to ensure that the resulting pixel values stay within valid intensity ranges, usually between 0 and 255.
- ↔️ After each convolution step, the kernel shifts over the image, and the same process repeats across different coordinates.
- ✂️ When the kernel reaches image edges where no pixels exist, there are several ways to handle it: by using pixel values from the original image, duplicating edge pixels, or applying a constant value.
- 🎛️ Convolution can be applied for various tasks like noise reduction, edge detection, and image sharpening, with the kernel’s values determining the specific effect.
- 🧠 The difference in convolution results comes from the different kernel configurations, allowing the technique to perform multiple image enhancement operations.
Q & A
What is the purpose of convolution in image processing?
-Convolution in image processing is used to improve image quality by applying filters that manipulate pixel values based on neighboring pixels. It is essential in tasks such as noise reduction, edge detection, and image enhancement.
What is a kernel in convolution, and how is it used?
-A kernel is a matrix used in convolution to determine how surrounding pixel values affect a specific pixel. It is applied to the image to generate a new set of pixel values based on this interaction. Kernels can vary in size and are crucial in defining the filter's behavior.
How are kernel coordinates defined, and what is the significance of the origin?
-Kernel coordinates are defined based on their position relative to the image. The origin, typically at the center of the kernel, determines the alignment of the kernel with the image. This position is important because it affects the final outcome of the convolution process.
What is the difference between linear and non-linear filters in image processing?
-Linear filters, such as those used in convolution, modify pixel values based on a weighted sum of surrounding pixels. Non-linear filters, like median filters, are used for tasks like edge detection and remove noise by considering pixel relationships differently, often not relying on a linear combination.
How does convolution handle image edges or borders?
-Convolution can handle edges by either ignoring the pixels that fall outside the image, duplicating the values from the edge, or filling in constant values such as 0 (padding). This ensures that the convolution process is applied uniformly across the image.
Why is it important to apply clipping during the convolution process?
-Clipping is essential to ensure pixel intensity values remain within a valid range, usually between 0 and 255 for an 8-bit image. If a value exceeds the range, clipping brings it back within limits, preventing distorted or incorrect image output.
What is the process for applying a convolution kernel to an image?
-To apply a convolution kernel, you align the kernel with the image starting at a specific position (e.g., (0,0)). For each position, you multiply corresponding pixel values by the kernel’s coefficients and sum them to produce a new pixel value. This process is repeated as the kernel shifts across the entire image.
What are some common applications of convolution in image processing?
-Convolution is used for various image processing tasks such as noise reduction, edge detection, sharpening, and blurring. Different types of kernels are used depending on the desired effect, like Gaussian blur for smoothing or Sobel operators for edge detection.
How does the size of the kernel affect the convolution process?
-The size of the kernel affects the scope of pixel interactions. Larger kernels take into account a broader area of neighboring pixels, which can produce smoother or more significant transformations, while smaller kernels focus on more localized changes.
How does convolution differ from matrix multiplication?
-Convolution differs from standard matrix multiplication because it involves multiplying and summing values from corresponding positions in a grid, but it also shifts the kernel over the entire image. Matrix multiplication is a more straightforward linear combination of matrix elements without this shifting operation.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

TUGAS PEMROSESAN CITRA DIGITAL (RESUME TENTANG KONVOLUSI)
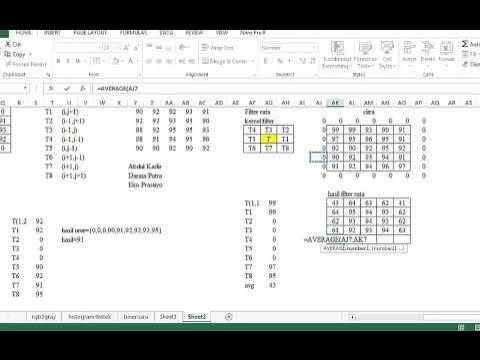
Materi Pengolahan Citra Digital|Filterin Rata|Filter Rata|Filter Rata di Matlab|nayavadaacademic.com

工程數學(一)期末報告 Group 5

Konvolusi Pengolahan Citra Digital | Secara Garis Besar #1
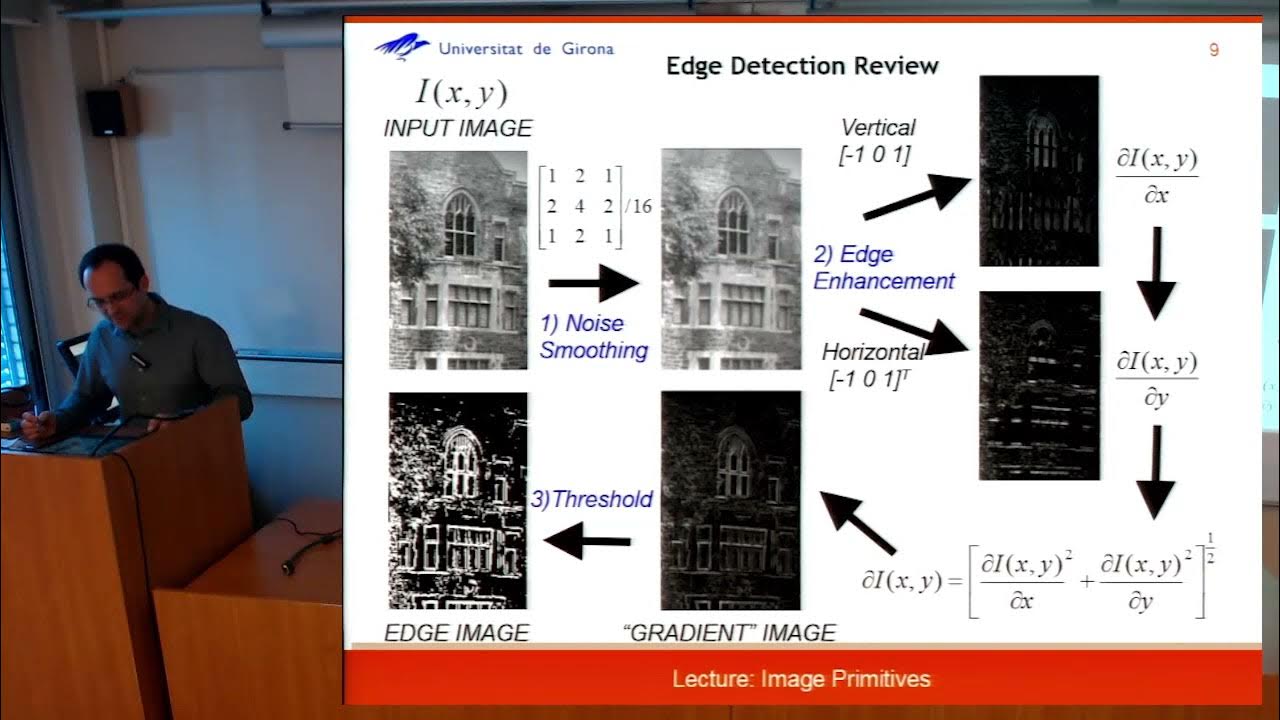
4 2 Filtering

Pertemuan 2 : Citra Digital, Sampling, dan Quantization - Part 1 : Apa itu citra digital ?
5.0 / 5 (0 votes)
