Electrical Engineering: Ch 18: Fourier Series (13 of 35) Even Periodic Functions
Summary
TLDRThe video script discusses simplifying the process of finding Fourier series coefficients for even periodic functions. It explains that even functions, which are symmetrical about the vertical axis, can be mirrored to produce duplicates on the other side. For such functions, the Fourier series involves only cosine terms, as sine terms become zero. The coefficients are calculated by integrating over half the period, doubling the amplitude, which simplifies the process significantly.
Takeaways
- 🔢 Recognizing the type of function (even or odd) simplifies finding the Fourier series.
- 🔄 Even periodic functions resemble cosine functions with symmetry about the vertical axis.
- ↔️ An even function remains the same if you replace the independent variable T with -T.
- 🔍 Examples of even periodic functions show identical behavior on both sides of the vertical axis.
- ✖️ When calculating Fourier coefficients for even functions, integrate only over half the period.
- 🧮 The coefficient a₀ is calculated as 2/T, with integration over half the period.
- 💡 The aₙ coefficients are found using a 4/T factor, only integrating over half the period.
- 🚫 For even functions, the Bₙ coefficients always equal zero, making the calculations simpler.
- ⏩ No need to compute Bₙ terms when working with even periodic functions, saving time.
- 📈 The symmetry of even functions helps streamline Fourier series calculations.
Q & A
What is an even function in the context of Fourier series?
-An even function in the context of Fourier series is a function that is symmetric about the vertical axis. If you take one side of the function and flip it over, it should look exactly the same on the other side.
How does the property of an even function relate to cosine functions?
-Even functions have properties similar to cosine functions because they both exhibit symmetry about the vertical axis. This means that if you replace every independent variable T with -T, you get the same function.
What is the significance of even periodic functions in Fourier series?
-Even periodic functions are significant in Fourier series because they allow for a simplification in calculating coefficients. The symmetry means that only cosine terms (a_n) need to be calculated, and sine terms (b_n) are zero.
How does the integration process differ for even functions when calculating Fourier coefficients?
-For even functions, the integration for calculating coefficients a_n only needs to be done over half the period instead of the entire period, and the amplitude is doubled. This is due to the symmetry of the function.
Why are the b_n coefficients zero for even functions?
-The b_n coefficients are zero for even functions because the function does not have any odd symmetry, which is required for sine terms in the Fourier series. Since even functions are symmetric about the vertical axis, there are no sine components.
Can you provide an example of an even periodic function?
-Yes, an example of an even periodic function could be a cosine function itself, like cos(ωt), or any function that is symmetric about the y-axis and repeats its values over a period.
What is the formula for calculating a_n coefficients for even functions?
-The formula for calculating a_n coefficients for even functions in the Fourier series is \( a_n = \frac{2}{T} \int_{0}^{T/2} f(t) \cos(n\omega t) dt \), where T is the period of the function.
How does the script suggest simplifying the process of finding Fourier coefficients for even functions?
-The script suggests that when dealing with even functions, you can ignore the calculation of b_n coefficients altogether since they are zero, and only calculate the a_n coefficients.
What is the implication of not having to calculate b_n coefficients for even functions?
-Not having to calculate b_n coefficients for even functions simplifies the process of finding the Fourier series representation of the function, as it reduces the number of integrals that need to be computed.
How does the script explain the process of flipping a function to determine if it's even?
-The script explains that to determine if a function is even, you can visualize flipping one side of the function over the vertical axis and see if it matches the other side, or mathematically replace T with -T and check if the function remains the same.
What is the role of the vertical axis in determining the evenness of a function?
-The vertical axis plays a crucial role in determining the evenness of a function because it serves as the line of symmetry. A function is even if it is symmetric about the vertical axis.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

TuMT 221 Tutorial Matematika Teknik - Deret Fourier Trigonometri
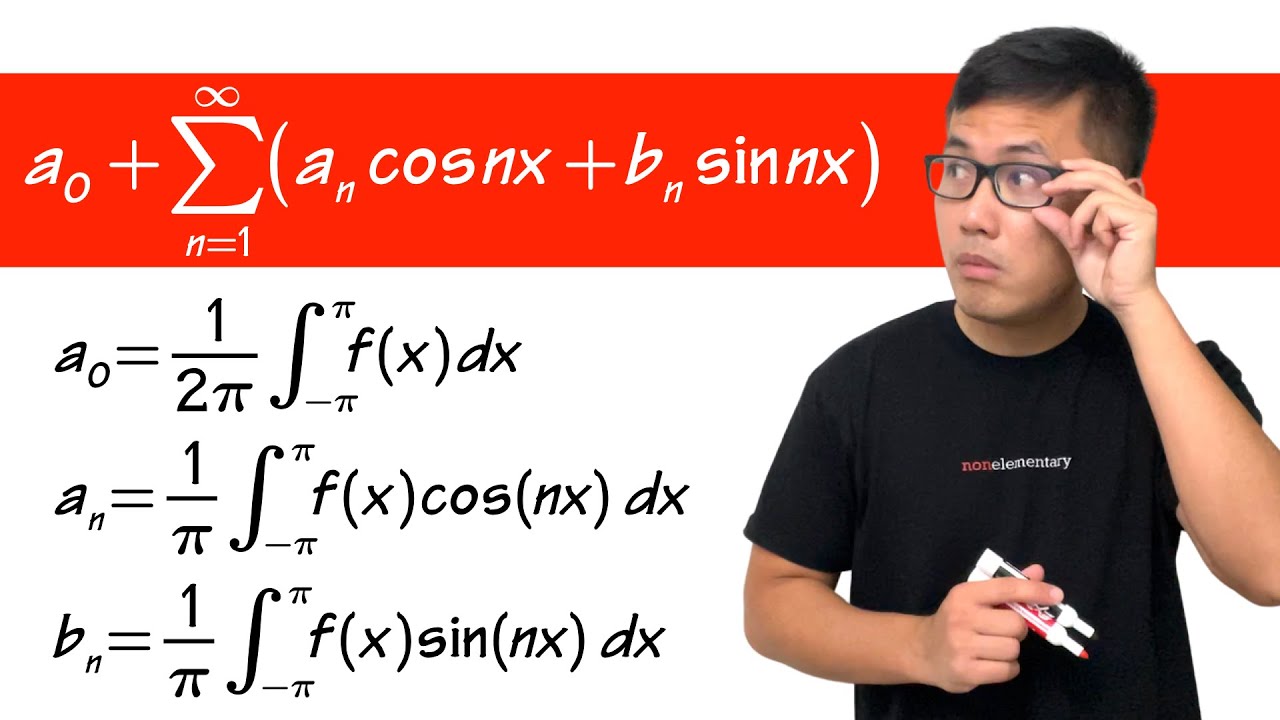
how to get the Fourier series coefficients (fourier series engineering mathematics)

I Prodigi della TRASFORMATA di FOURIER

FOURIER SERIES LECTURE 2 | STUDY OF FORMULAS OF FOURIER SERIES AND PERIODIC FUNCTION

Introduction to Fourier Series | Trigonometric Fourier Series Explained

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY
5.0 / 5 (0 votes)
