Introduction to Fourier Series | Trigonometric Fourier Series Explained

Summary

In this video, the concept of Fourier Series is explained, focusing on its role in analyzing the frequency spectrum of periodic signals. The presenter covers the basics of harmonics, orthogonality, and how the Trigonometric Fourier Series can represent any periodic signal as a sum of sine and cosine waves. Through a vector analogy, the video illustrates how these orthogonal signals minimize the error in signal approximation. The session concludes with an overview of the Fourier coefficients and their significance in analyzing the components of a signal, setting the stage for future discussions on the exponential Fourier Series.

Takeaways

• 😀 Fourier Series helps us represent any periodic signal as a combination of sine and cosine waves.
• 😀 A periodic signal can be analyzed in terms of its frequency spectrum using Fourier analysis, which reveals the signal’s frequency content.
• 😀 The fundamental frequency of a periodic signal is the inverse of its time period (1/T), and harmonics are integer multiples of this fundamental frequency.
• 😀 The Trigonometric Fourier Series expresses periodic signals using sinusoidal components (sine and cosine waves) of the fundamental frequency and its harmonics.
• 😀 The Fourier Series coefficients (ao, An, Bn) represent the amplitude of the corresponding sine and cosine waves in the series.
• 😀 The sine and cosine waves used in Fourier Series are orthogonal, meaning their dot product is zero, which allows them to uniquely represent any periodic signal.
• 😀 The energy of the error signal in Fourier Series approximation is minimized when the error is perpendicular to the signal components (orthogonality).
• 😀 The value of the Fourier coefficient c in a signal’s approximation is determined by the ratio of the dot product of the signal and the base function to the dot product of the base function with itself.
• 😀 The concept of orthogonality in vectors is similar to orthogonality in signal components, allowing for error-free representation of a signal when using a complete set of orthogonal functions.
• 😀 Cosine and sine waves and their harmonics form a complete set of orthogonal signals, meaning any periodic signal can be expressed as a linear combination of these orthogonal components.
• 😀 The Trigonometric Fourier Series allows us to analyze the frequency components of any periodic signal, with each harmonic contributing a distinct weight to the overall signal.

Q & A

What is the main topic of the video?

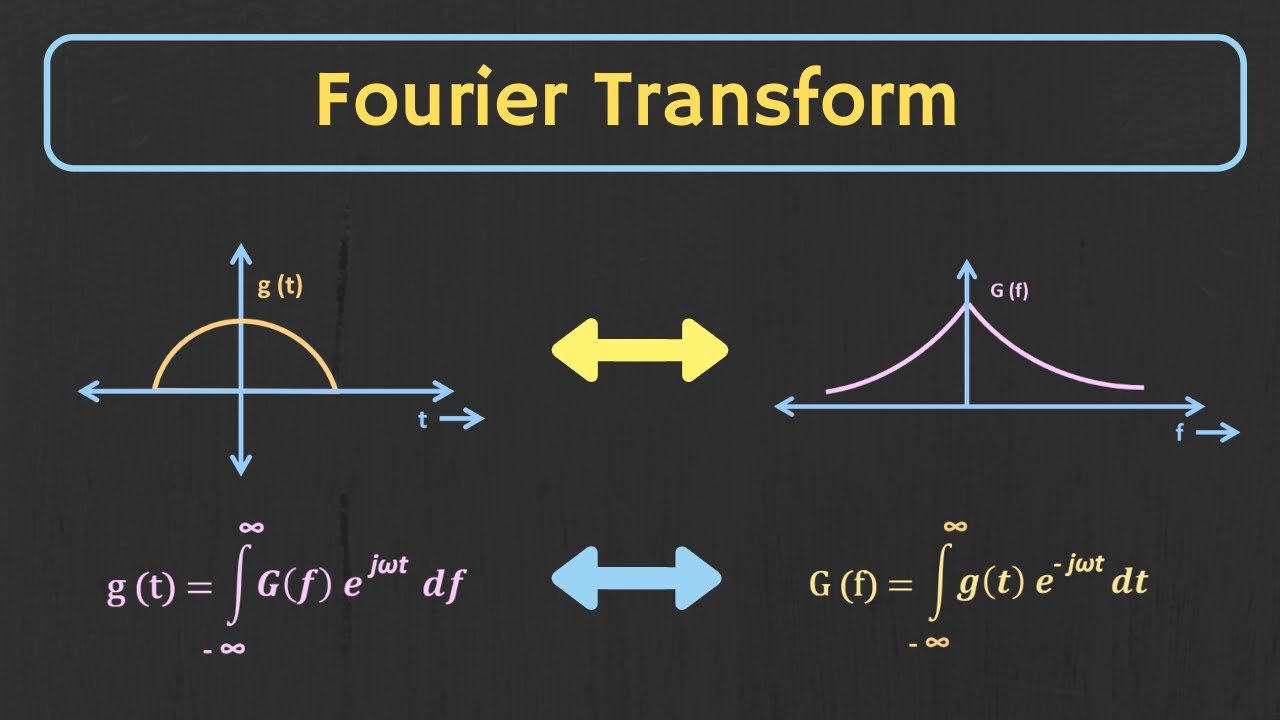
The main topic of the video is the Fourier Series, specifically the Continuous-Time Fourier Series, and how it can be used to analyze and represent periodic signals in terms of sine and cosine waves.

Why is it important to understand the frequency spectrum of a signal?

Understanding the frequency spectrum of a signal is crucial because it provides insight into the different frequency components within the signal, which is essential for communication systems and signal processing.

What is the Fourier Series used for in signal analysis?

The Fourier Series is used to represent any periodic signal as a sum of sine and cosine waves, allowing us to analyze the signal in terms of its frequency components.

What is the difference between Continuous-Time Fourier Series and Discrete-Time Fourier Series?

The Continuous-Time Fourier Series is used for periodic signals defined over continuous time, while the Discrete-Time Fourier Series is used for periodic signals defined in discrete time.

What are harmonics in the context of Fourier Series?

Harmonics are integer multiples of the fundamental frequency of a periodic signal. For example, if the fundamental frequency is 'f', the second harmonic will be '2f', the third harmonic will be '3f', and so on.

What is the significance of sine and cosine waves in the Fourier Series?

Sine and cosine waves are used as the basis functions in the Fourier Series because they are orthogonal, meaning their dot product is zero, which allows them to represent different frequency components of a signal without interference.

How does the concept of orthogonality apply to the Fourier Series?

In the Fourier Series, sine and cosine functions are orthogonal to each other, meaning that their dot product is zero. This orthogonality allows any periodic signal to be uniquely represented as a linear combination of these functions.

How are the coefficients in the Fourier Series (ao, An, Bn) determined?

The Fourier Series coefficients (ao, An, Bn) are determined by integrating the periodic signal with sine and cosine functions over one period. These coefficients represent the amplitude or weight of each sine and cosine wave in the signal's representation.

Why does the error in approximating a signal become minimal when using orthogonal functions?

When using orthogonal functions, the projection of a signal onto these functions minimizes the error because orthogonal functions do not overlap, ensuring the best approximation with minimal error in representing the signal.

What happens when the set of orthogonal signals is complete in the Fourier Series?

When the set of orthogonal signals is complete, the error in approximating the signal becomes zero, meaning the signal can be exactly represented as a linear combination of these orthogonal signals.