TuMT 221 Tutorial Matematika Teknik - Deret Fourier Trigonometri
Summary
TLDRThis tutorial on Fourier series in trigonometry explains how to represent periodic functions as sums of sines and cosines. The instructor walks through the process of determining the period and symmetry of a function, emphasizing how these affect the calculation of Fourier coefficients. The video covers the method for calculating these coefficients using integration, particularly for even and odd functions, using an example of a periodic triangular waveform. It highlights important aspects like integrating over the function's period and applying symmetry to simplify the process, making complex concepts accessible for students of engineering mathematics.
Takeaways
- 😀 The tutorial covers the concept of trigonometric series and Fourier series, explaining how periodic functions can be represented as trigonometric sums.
- 😀 The general form of a trigonometric series is introduced, which involves coefficients that can be determined through integration over the function's period.
- 😀 If a function is even, the sine coefficients (b_n) are zero, while if the function is odd, the cosine coefficients (a_n) are zero.
- 😀 When the function is neither even nor odd, all coefficients (a_n, b_n) must be calculated separately.
- 😀 For even functions, the Fourier series can be simplified by only considering half of the period, doubling the result afterward.
- 😀 The importance of recognizing the symmetry of the function is emphasized to determine which coefficients are non-zero.
- 😀 A graphical example of a periodic triangle wave is used to demonstrate the process of determining the function's period and symmetry.
- 😀 The period of the function in the example is determined by measuring the length of one full wave cycle.
- 😀 The script explains how to write the mathematical expressions of a periodic function using piecewise linear functions, focusing on calculating gradients and the equation of the line.
- 😀 The Fourier coefficients are calculated using integrals, with a detailed example involving integration by parts to evaluate the coefficients.
- 😀 The resulting Fourier series expansion is presented in a summation form, which represents the periodic function as a sum of cosines with different coefficients.
Q & A
What is the main topic of this tutorial?
-The main topic of the tutorial is the Fourier series, specifically focusing on trigonometric series for periodic functions.
What does the Fourier series represent for a periodic function?
-The Fourier series represents a periodic function as a sum of sinusoidal terms (sines and cosines) with different frequencies and amplitudes.
What is the general form of the Fourier series presented in the tutorial?
-The general form of the Fourier series presented is: FT(t) = a₀/2 + Σ (aₙ * cos(nω₀t) + bₙ * sin(nω₀t)) where the sum runs from n = 1 to infinity.
How do you calculate the Fourier coefficients (aₙ and bₙ)?
-The Fourier coefficients are calculated using integrals over one period of the function. The formulas are: aₙ = (2/T) * ∫[F(t) * cos(nω₀t) dt] and bₙ = (2/T) * ∫[F(t) * sin(nω₀t) dt], where T is the period of the function.
What is the significance of recognizing whether a function is odd or even?
-Recognizing whether a function is odd or even allows for simplifications in the Fourier series. For even functions, the bₙ coefficients will be zero, and for odd functions, the aₙ coefficients will be zero.
How can we simplify the Fourier series calculation for even or odd functions?
-For even functions, we only need to calculate aₙ coefficients as bₙ will be zero. For odd functions, we only calculate bₙ coefficients, and aₙ will be zero. This reduces the complexity of the calculations.
What is the period of the triangular waveform used in the example problem?
-The period of the triangular waveform is 2, as indicated in the tutorial where the function repeats every two units.
How do you identify whether a function is even or odd from its graph?
-A function is even if it is symmetric about the y-axis. It is odd if it has symmetry about the origin (i.e., the function satisfies F(-t) = -F(t)).
What is the benefit of calculating the Fourier series for a triangular waveform?
-The benefit is that the Fourier series allows us to express the triangular waveform as a sum of sinusoidal functions, which is useful in various engineering and signal processing applications.
What steps are involved in calculating the Fourier series for a triangular function from the example?
-The steps involve: 1) Identifying the period and symmetry of the function, 2) Writing the function as a mathematical expression, 3) Calculating the Fourier coefficients aₙ and bₙ using integrals, and 4) Combining these coefficients to form the complete Fourier series.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
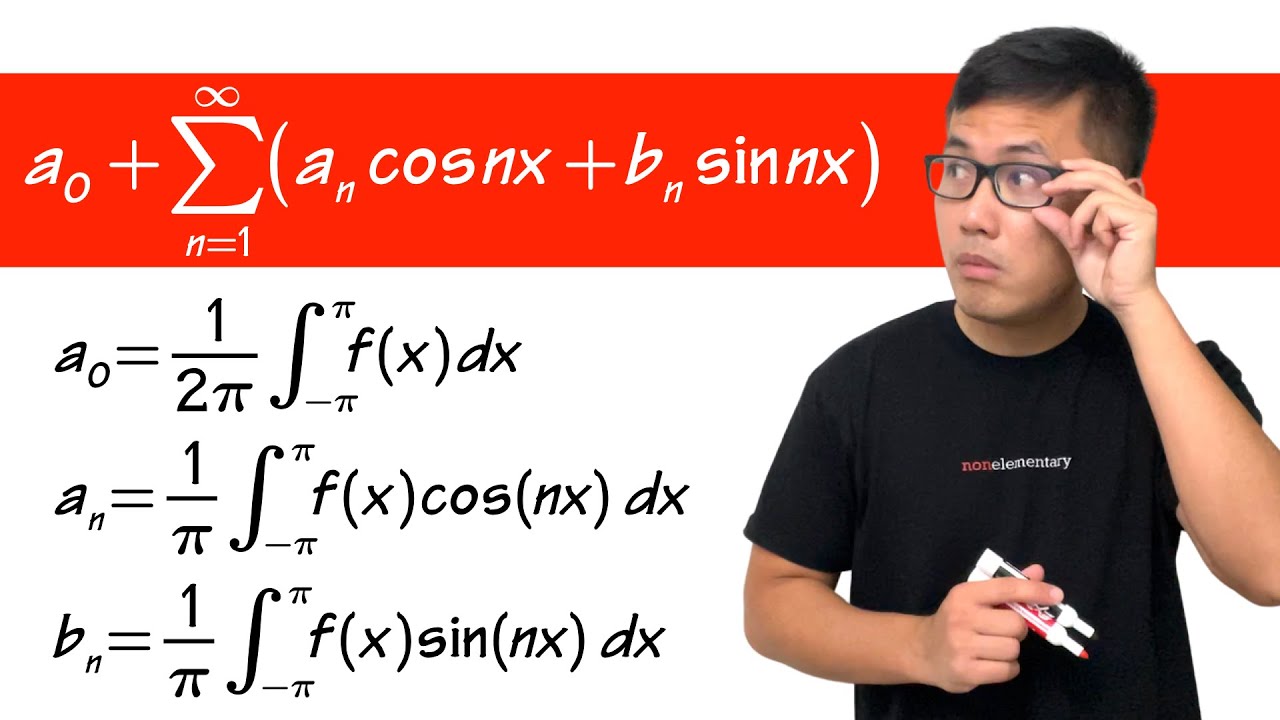
how to get the Fourier series coefficients (fourier series engineering mathematics)

The Fourier Transform in 15 Minutes

Introduction to Fourier Series | Trigonometric Fourier Series Explained

Intro to FOURIER SERIES: The Big Idea

FOURIER SERIES LECTURE 2 | STUDY OF FORMULAS OF FOURIER SERIES AND PERIODIC FUNCTION

I Prodigi della TRASFORMATA di FOURIER
5.0 / 5 (0 votes)