I Prodigi della TRASFORMATA di FOURIER
Summary
TLDRThis video explores the profound insights of the Fourier Transform, illustrating how it allows for the decomposition of any waveform into an infinite sum of sine and cosine functions. It introduces key concepts like the Fourier series for periodic phenomena and the transition to the Fourier Transform for non-periodic functions. The video explains the significance of Fourier coefficients, spectral analysis, and the relationship between time and frequency domains. Additionally, it highlights practical applications, from quantum mechanics to digital image processing, showcasing the transformative power of Fourier analysis in understanding complex waveforms.
Takeaways
- 😀 The Fourier Transform is one of the deepest insights into understanding how various phenomena can be represented as waves.
- 📊 Any wave can be decomposed into an infinite sum of sine and cosine functions, revealing a universal principle discovered by Fourier in the early 19th century.
- 🔄 The Fourier Series allows us to represent periodic phenomena by decomposing them into their sinusoidal components.
- ⏰ The period of a wave is the characteristic time after which the physical pattern of a vibrating object repeats itself.
- 🔍 The Fourier Transform takes a time-domain function and converts it into a frequency-domain representation, revealing the spectral components of the signal.
- 📐 The Fourier Transform can be expressed as an integral, which operates in a continuous domain as opposed to the discrete nature of Fourier Series.
- 🔄 The inverse Fourier Transform allows us to reconstruct the original time-domain function from its frequency-domain representation.
- 🎶 The Fourier Transform is akin to a scanner that analyzes a function to determine which frequencies contribute to forming the original signal.
- 📉 The results of the Fourier Transform are complex numbers, representing both the amplitude and phase information of the sinusoidal components.
- 🖥️ The Fast Fourier Transform (FFT) is an efficient algorithm for computing the Fourier Transform, widely used in various applications including data processing, signal analysis, and image compression.
Q & A
What is the significance of the Fourier Transform in mathematics?
-The Fourier Transform is a fundamental mathematical concept that allows for the decomposition of any waveform into a sum of infinite sinusoidal functions, thereby enabling the analysis of signals in the frequency domain.
How does the Fourier Transform relate to periodic and non-periodic functions?
-For periodic functions, the decomposition is achieved using the Fourier Series, while for non-periodic functions, the Fourier Transform is utilized to analyze the signal in terms of its frequency components.
What is the mathematical representation of the Fourier Transform?
-The Fourier Transform is mathematically defined as: F(ω) = ∫_{-∞}^{∞} f(t)e^{-jωt} dt, where f(t) is the time-domain signal and F(ω) is its frequency-domain representation.
What properties does the Fourier Transform exhibit?
-The Fourier Transform exhibits several properties including linearity, time and frequency shifts, and correlation, which facilitate the manipulation and understanding of signals.
What is the purpose of the Inverse Fourier Transform?
-The Inverse Fourier Transform allows for the reconstruction of the original time-domain signal from its frequency-domain representation, enabling the analysis of signals after transformation.
Can you explain the relationship between the Fourier Transform and the Laplace Transform?
-The Fourier Transform can be seen as a special case of the Laplace Transform, specifically when evaluated along the imaginary axis, highlighting their interconnectedness in signal processing.
What are some practical applications of the Fourier Transform?
-The Fourier Transform is widely used in fields such as quantum mechanics, electrical engineering, data processing, audio signal processing, and image compression techniques like JPEG.
How does the Fourier Transform analyze wave phenomena?
-The Fourier Transform analyzes wave phenomena by decomposing signals into their constituent frequencies, allowing for the identification and quantification of different frequency components present in the signal.
What is the role of the exponential function in the Fourier Transform?
-The exponential function in the Fourier Transform (e^{-jωt}) encapsulates all the information about the wave phenomenon being analyzed, acting as a core element that enables frequency analysis.
How does the Fourier Transform help in digital signal processing?
-In digital signal processing, the Fourier Transform is crucial for analyzing, filtering, and reconstructing signals, making it an essential tool for various applications, from communications to audio and image processing.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY

Identidades trigonométricas, Identidades de simetría e identidades de suma y resta.
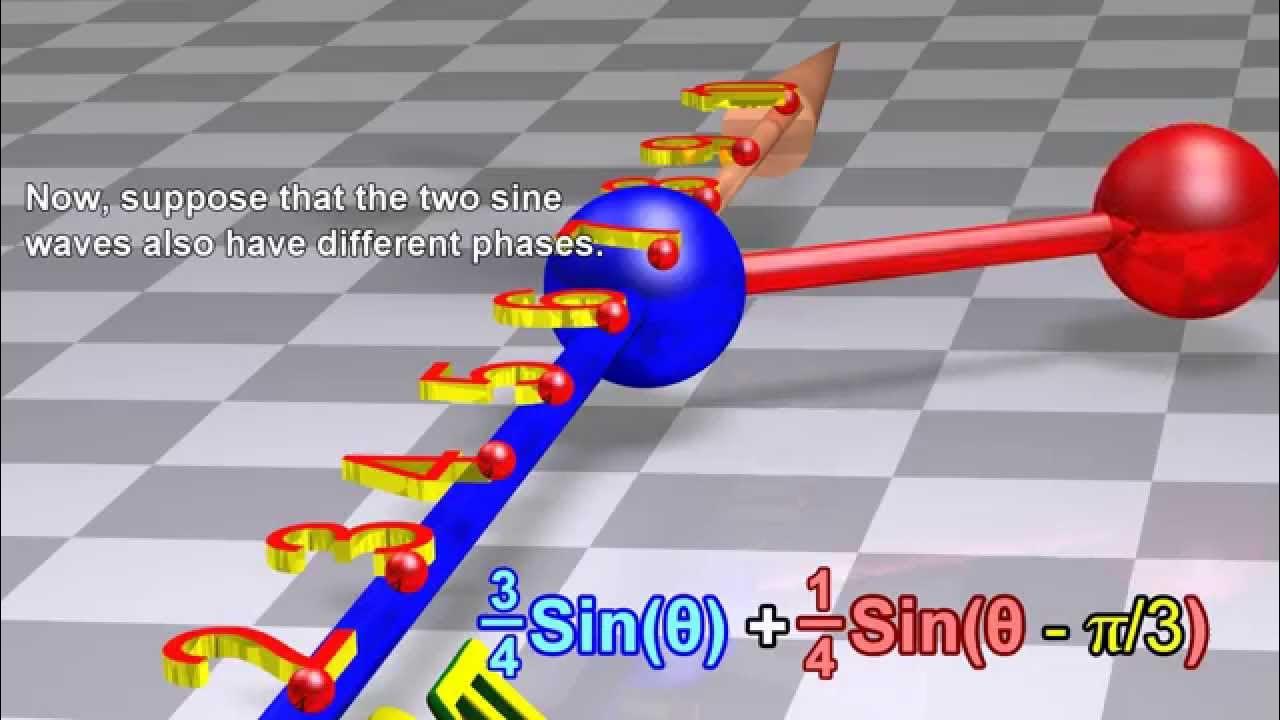
Fourier Transform, Fourier Series, and frequency spectrum
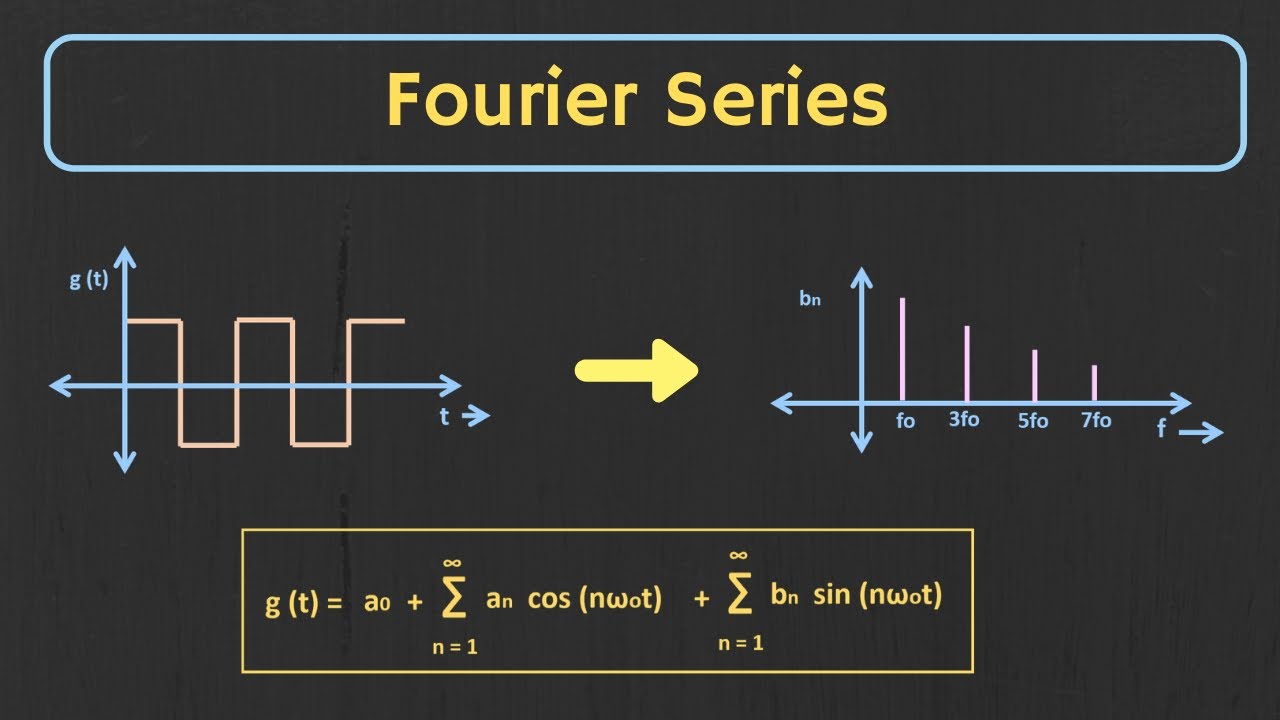
Introduction to Fourier Series | Trigonometric Fourier Series Explained
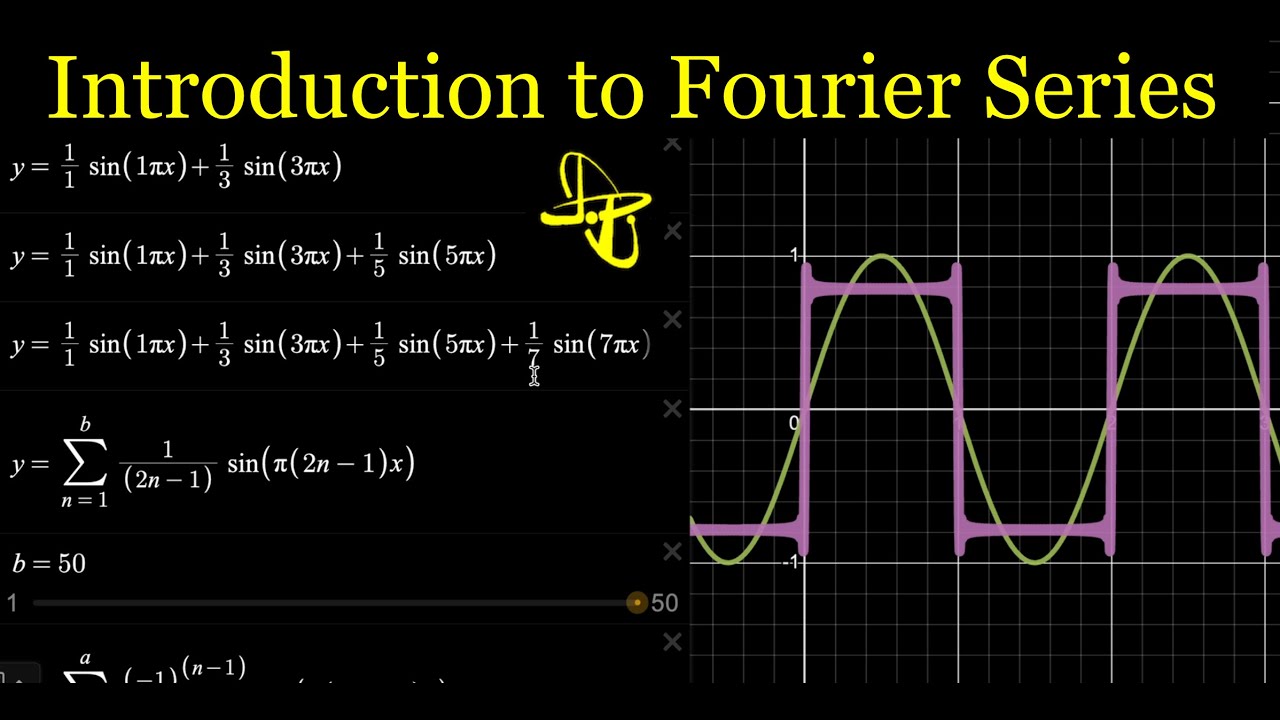
Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves

LECTURE 13 - FOURIER TRANSFORMATION IN DIGITAL IMAGE PROCESSING | GATE GEOMATICS ENGINEERING | #gate
5.0 / 5 (0 votes)