FOURIER SERIES LECTURE 2 | STUDY OF FORMULAS OF FOURIER SERIES AND PERIODIC FUNCTION
Summary
TLDRThis educational video from the Akaademy YouTube channel focuses on the definition of periodic functions and the formula for Fourier series. The instructor explains the criteria for a function to be periodic, using the example of f(x) and its period T. They also cover the necessary conditions for a function to have a Fourier series, known as Dirichlet's conditions. The video then delves into the standard formula for Fourier series, explaining how to calculate the coefficients a_n and b_n. The instructor emphasizes the importance of understanding these concepts to solve problems involving Fourier series effectively.
Takeaways
- 😀 The video is part of a series on the topic of Fourier Series, specifically focusing on the definition of periodic functions and the formula for Fourier Series.
- 📚 The audience is expected to have a basic understanding of the previous lectures on the topic, including the definition of Fourier Series and its basic points.
- 🔢 A function f(x) is defined as periodic if f(x + T) = f(x) for every x in its domain, where T is a positive constant called the period.
- 🌐 The concept of the period T is crucial, and functions like sin(x) and cos(x) are given as examples of periodic functions with a period of 2π.
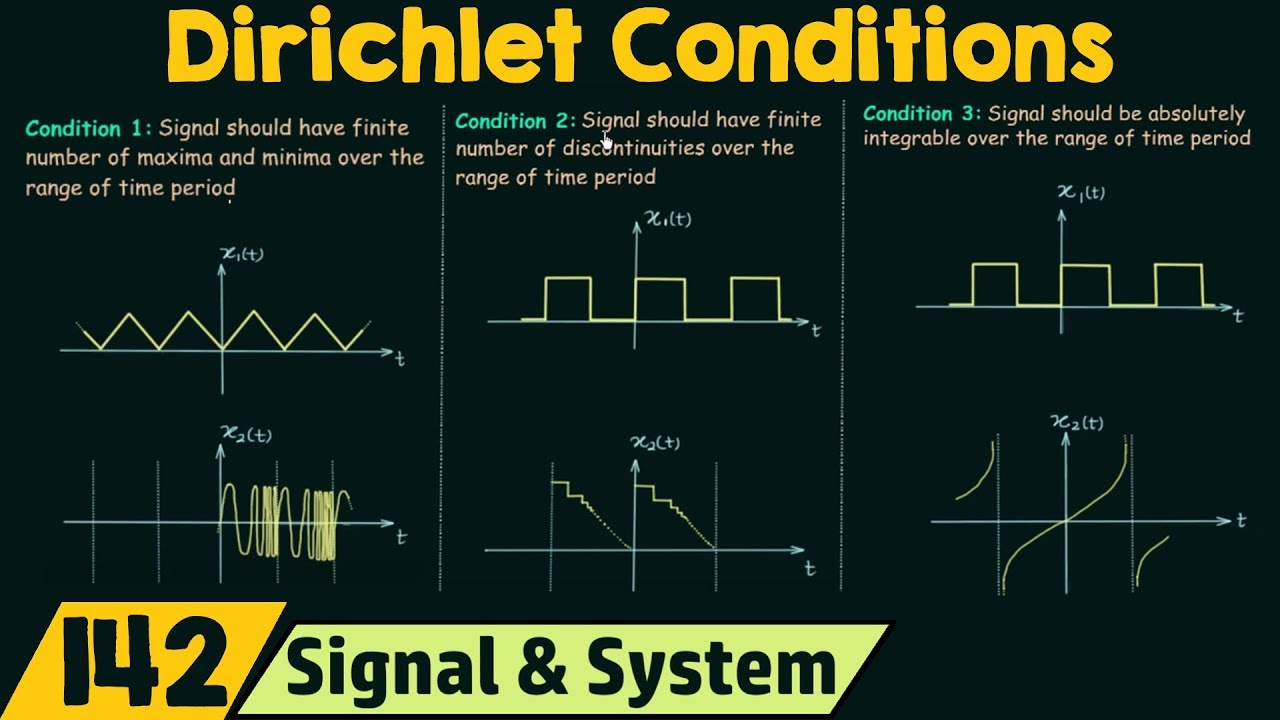
- 📐 The video emphasizes the importance of satisfying certain conditions, known as Dirichlet's conditions, for a function to have a Fourier Series.
- 🔑 Dirichlet's conditions include the function being single-valued, having a finite number of discontinuities, and a finite number of extrema within any period.
- 📘 The formula for the Fourier Series is provided, which includes terms for a0/2, and the sum of an and bn coefficients multiplied by cos(nπx/L) and sin(nπx/L) respectively.
- 🔍 The video explains how to find the coefficients an and bn through integration over the interval [c, c + 2L], where c and L are specific values related to the period.
- 📊 The script provides an example to illustrate how changes in the period affect the formula for the Fourier Series coefficients.
- 🎓 The video concludes by summarizing the key points covered, including the definition of periodic functions and the Fourier Series formula, and encourages the audience to note these down for future reference.
Q & A
What is the main topic of the video?
-The main topic of the video is the study of periodic functions and the Fourier series formula.
What is a periodic function?
-A periodic function is defined as a function f(x) that satisfies the condition f(x + T) = f(x) for some positive constant T, called the period.
What are the conditions for a function to be considered periodic?
-A function is considered periodic if it satisfies the condition f(x + T) = f(x) for all x in its domain, where T is a positive constant.
What is the period T in the context of the video?
-In the video, the period T is a positive constant that defines the repeating interval of a periodic function.
What are the Dirichlet conditions mentioned in the video?
-The Dirichlet conditions are three criteria that a function must satisfy to have a Fourier series. They include: 1) The function must be single-valued, 2) The function must have a finite number of discontinuities, and 3) The function must have a finite number of extrema in any interval.
What are the two important functions discussed in the video that are periodic?
-The two important periodic functions discussed are sin(x) and cos(x).
What is the standard formula for the Fourier series?
-The standard formula for the Fourier series of a function f(x) is given by f(x) = a0/2 + Σ[an * cos(nπx/L) + bn * sin(nπx/L)], where an and bn are the Fourier coefficients.
How are the Fourier coefficients an and bn calculated?
-The Fourier coefficients an and bn are calculated using integration over one period of the function. Specifically, an = (1/L) * ∫[f(x) * cos(nπx/L)] dx from 0 to L, and bn = (1/L) * ∫[f(x) * sin(nπx/L)] dx from 0 to L.
What is the significance of the lower and upper limits of integration in the Fourier coefficients formula?
-The lower and upper limits of integration in the Fourier coefficients formula represent one period of the function, which is crucial for calculating the coefficients accurately.
How does the period of a function affect the calculation of its Fourier series?
-The period of a function directly affects the calculation of its Fourier series because the coefficients an and bn are calculated over one period of the function, and the formula changes accordingly if the period is different from the standard 2π.
What is the next topic to be covered in the series after the Fourier series?
-The next topic to be covered in the series is even functions and odd functions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY

I Prodigi della TRASFORMATA di FOURIER
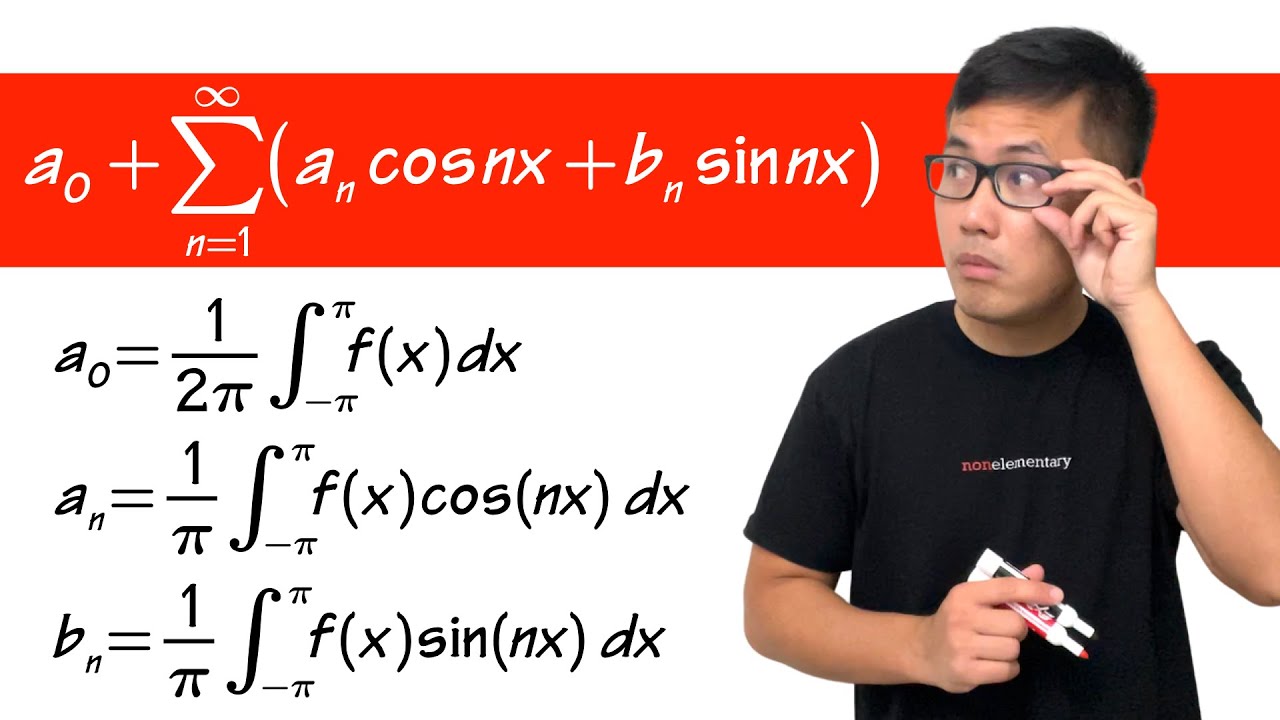
how to get the Fourier series coefficients (fourier series engineering mathematics)

TuMT 221 Tutorial Matematika Teknik - Deret Fourier Trigonometri

Electrical Engineering: Ch 18: Fourier Series (13 of 35) Even Periodic Functions
Conditions for Existence of Fourier Series (Dirichlet Conditions)
5.0 / 5 (0 votes)