Kinematic Equations in One Dimension | Physics with Professor Matt Anderson | M2-04

Summary

This lecture introduces the fundamental kinematic equations for motion in one dimension (1D) with constant acceleration. The key equations describe position, velocity, and acceleration over time, focusing on free fall as an example. The professor walks through the calculus derivations of each equation, emphasizing the relationship between position, velocity, and acceleration. A specific case of vertical motion under gravity is explored, showing how an object falls with a quadratic position function and linear velocity increase. The session also touches on the importance of constant acceleration in these equations, which are crucial for analyzing basic motion.

Takeaways

• 😀 Kinematic equations describe motion in one dimension under the assumption of constant acceleration.
• 😀 The main 1D kinematic equations are for position, velocity, and the relationship between velocity and position.
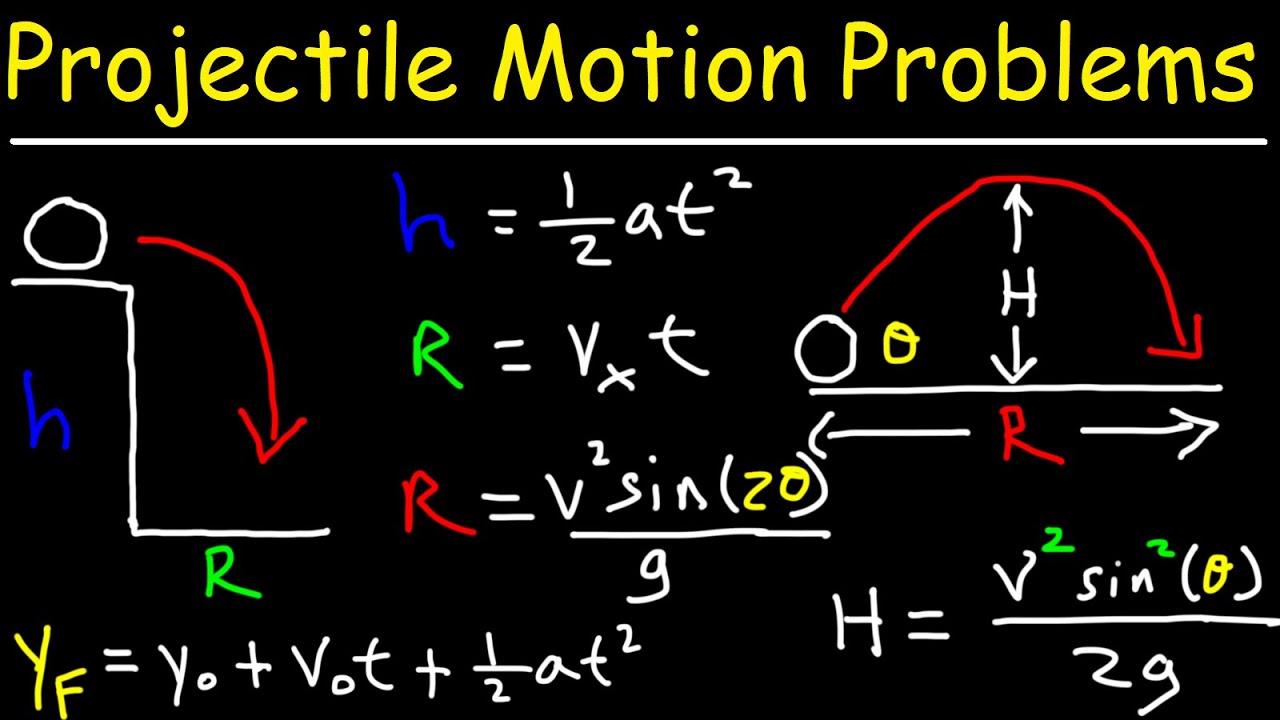
• 😀 Position equation: x_f = x_i + v_xi * t + 1/2 * a_x * t^2, derived from integrating acceleration twice.
• 😀 Velocity-time equation: v_xf = v_xi + a_x * t, derived from integrating acceleration once.
• 😀 Velocity-position equation: v_xf^2 = v_xi^2 + 2 * a_x * (x_f - x_i), derivable from other kinematic equations or energy conservation.
• 😀 For vertical motion, the position of a free-falling object is y(t) = h - 1/2 * g * t^2, with downward motion indicated by a negative sign.
• 😀 Velocity is the derivative of position; for free fall, v_y = -g * t, increasing linearly over time.
• 😀 Acceleration is the derivative of velocity; in free fall, a_y = -g, which is constant near Earth's surface.
• 😀 Free-fall motion has a constant downward acceleration, linearly increasing velocity, and quadratically changing position.
• 😀 The kinematic equations are only valid for constant acceleration and near Earth's surface where gravity is approximately constant.
• 😀 Using calculus allows derivation of velocity and acceleration from position functions, reinforcing the relationship between these quantities.

Q & A

What is the key assumption made about acceleration in 1D kinematic equations?

The key assumption is that acceleration is constant. If acceleration is not constant, the standard kinematic equations cannot be applied.

What is the kinematic equation for position as a function of time?

The position equation is: x_final = x_initial + v_initial * t + 1/2 * a * t^2, where x_initial is the initial position, v_initial is the initial velocity, a is constant acceleration, and t is time.

How can you derive the velocity equation from constant acceleration?

By integrating the constant acceleration a with respect to time, you get the velocity equation: v_final = v_initial + a * t.

What is the equation that relates velocity squared to displacement?

The equation is v_final^2 = v_initial^2 + 2 * a * (x_final - x_initial), which can also be derived using energy conservation principles.

How is vertical motion represented in the transcript example?

Vertical motion is represented with y as a function of time, starting from height h and moving downward to y = 0. The equation used is y(t) = h - 1/2 * g * t^2, where g is the acceleration due to gravity.

How is velocity related to position in calculus terms?

Velocity is the derivative of position with respect to time. For the vertical motion example, v_y = dy/dt = -g * t.

What does the negative sign in the vertical velocity equation indicate?

The negative sign indicates that the object is moving in the negative y direction, meaning it is falling downward.

How is acceleration related to velocity?

Acceleration is the derivative of velocity with respect to time. For free fall, the derivative of velocity v_y = -g * t gives a constant acceleration a = -g.

What is the magnitude of acceleration due to gravity near the Earth's surface?

The acceleration due to gravity near the Earth's surface is approximately 9.8 meters per second squared (m/s^2).

How do position, velocity, and acceleration change over time for an object in free fall?

In free fall, the object's position changes quadratically over time, velocity increases linearly, and acceleration remains constant at -g.

Why can't kinematic equations for constant acceleration be applied at higher altitudes?

At higher altitudes, the acceleration due to gravity changes because it decreases slightly with distance from the Earth's surface, violating the constant acceleration assumption.