PHYS 121 - Week 6 Lecture 2 - Rotational Motion

Summary

This lecture focuses on rotational motion, covering key concepts such as angular displacement, angular velocity, and angular acceleration. The discussion delves into how these quantities behave as vectors, emphasizing the relationship between linear and angular variables. The lecture also explores how constant angular acceleration affects rotational motion and how linear motion concepts can be applied to rotational systems. Practical examples, including kinematic equations for angular motion, tangential velocity, and radial acceleration, help clarify the connections between linear and angular quantities, highlighting their applications in real-world scenarios like rotating objects.

Takeaways

• 😀 Rotational motion involves understanding rotational quantities such as angular displacement, angular velocity, and angular acceleration.
• 😀 The order of vector addition does not affect the sum for small angular displacements, but large angular displacements do not behave as simple vectors.
• 😀 The right-hand rule is used to determine the direction of angular velocity and angular acceleration, depending on whether the rotation is speeding up or slowing down.
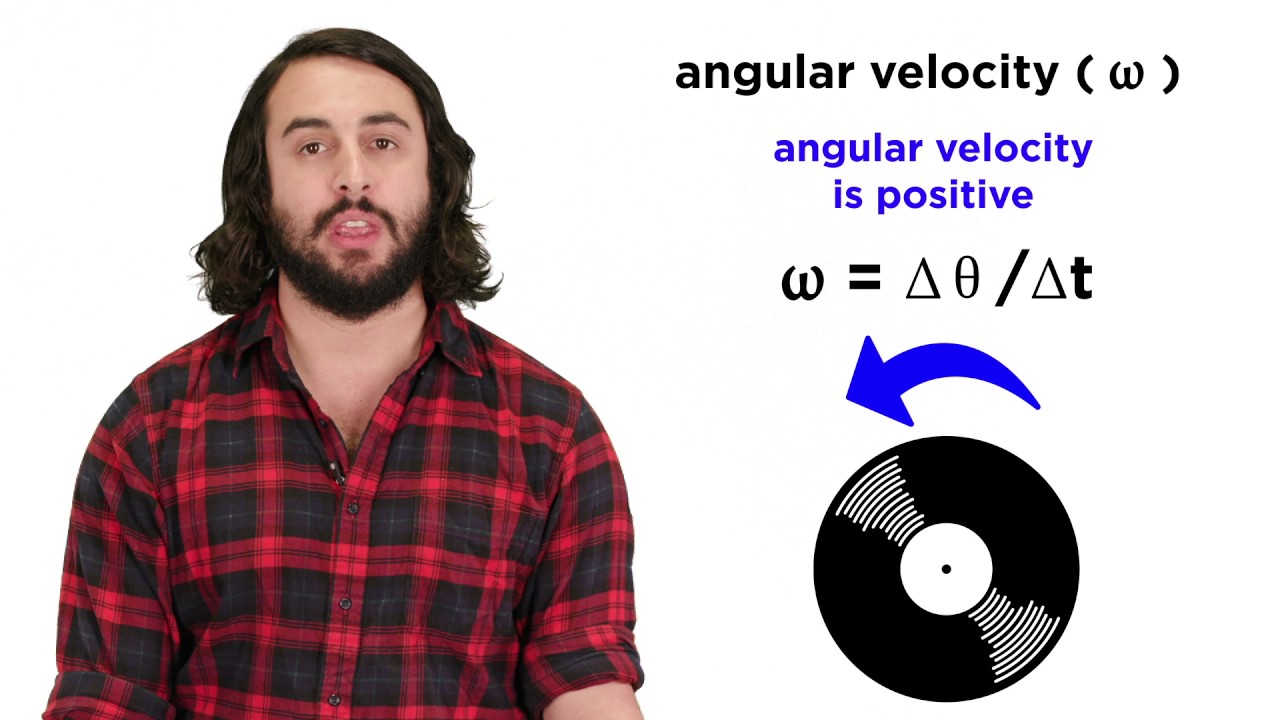
• 😀 Angular velocity is defined as the time derivative of angular position and is a vector quantity pointing along the axis of rotation.
• 😀 Rotational motion is analogous to linear motion, where angular variables like angular velocity and angular acceleration correspond to linear velocity and acceleration.
• 😀 The relationship between linear and angular variables is expressed by equations like tangential velocity = angular velocity * radius, and tangential acceleration = angular acceleration * radius.
• 😀 Radial acceleration is the acceleration towards the center of a circular path and is given by the formula: radial acceleration = angular velocity^2 * radius.
• 😀 The total acceleration in rotational motion is a vector sum of radial (centripetal) and tangential accelerations, with each affecting the motion differently.
• 😀 In problems involving constant angular acceleration, standard kinematic equations for angular motion can be used, similar to linear motion equations.
• 😀 In a sample problem, angular displacement, angular speed, and tangential quantities like velocity, acceleration, and radial acceleration were calculated for a rotating grindstone.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.