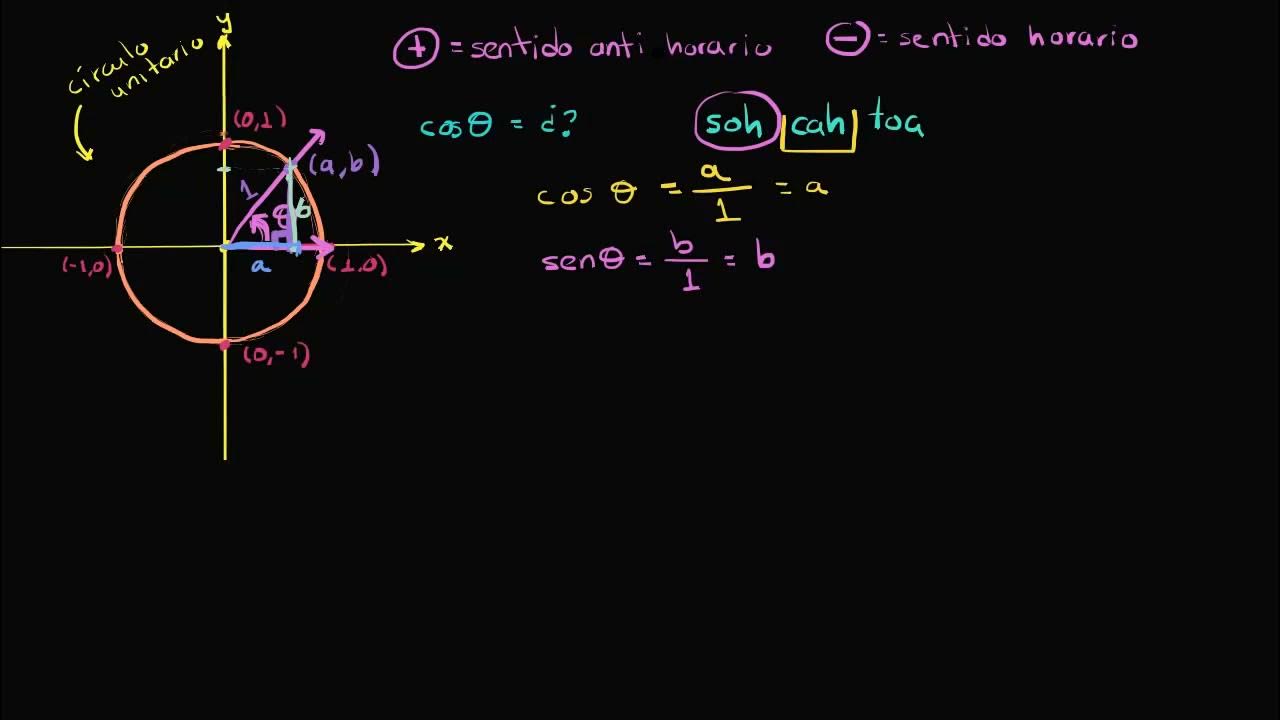TRIGONOMETRY 1 (PRECALCULUS) (1 of 54) What Is The Unit Circle?
Summary
TLDRThis video introduces the fundamentals of trigonometry through the concept of the unit circle. It explains the relationship between the sides of a triangle and angles, defining key terms such as radians and degrees. The unit circle, centered at the origin with a radius of one, is central to understanding trigonometric relationships. The video covers the circumference of the circle, the significance of angles like π/4 radians, and how to calculate coordinates on the unit circle. This foundational knowledge serves as a stepping stone for further studies in trigonometry.
Takeaways
- 😀 The unit circle is a fundamental concept in trigonometry, representing a circle with a radius of one centered at the origin.
- 📐 The equation of the unit circle is expressed as x² + y² = 1, illustrating the relationship between the x and y coordinates.
- 🔄 A full rotation around the unit circle corresponds to an angle of 360 degrees or 2π radians.
- ⚖️ Radians are a dimensionless unit for measuring angles, commonly used in trigonometry, with 2π radians being equivalent to the circumference of the circle.
- 📏 An angle of π/4 radians (or 45 degrees) results in equal x and y values on the unit circle.
- ➗ At π/4 radians, the coordinates on the unit circle are (√2/2, √2/2), indicating both sine and cosine values at this angle.
- 📊 The distance traveled along the circumference corresponding to an angle can be calculated using the formula s = θr, where θ is in radians.
- 🧮 The Pythagorean theorem can be applied to find relationships between the sides of triangles formed in the unit circle.
- 🔺 The triangle formed with a 45-degree angle shows perfect symmetry, leading to equal side lengths for x and y.
- 💡 Understanding these relationships is crucial for grasping more advanced trigonometric concepts and applications.
Q & A
What is the primary focus of trigonometry as described in the video?
-The primary focus of trigonometry is the relationship between the sides of a triangle and the angles formed between those sides.
What is the unit circle, and why is it significant in trigonometry?
-The unit circle is a circle with a radius of one unit centered at the origin. It is significant because it provides a foundation for defining trigonometric functions and understanding their relationships with angles and side lengths.
How is the equation of the unit circle expressed mathematically?
-The equation of the unit circle is expressed as x² + y² = 1, where x and y are the coordinates of points on the circle.
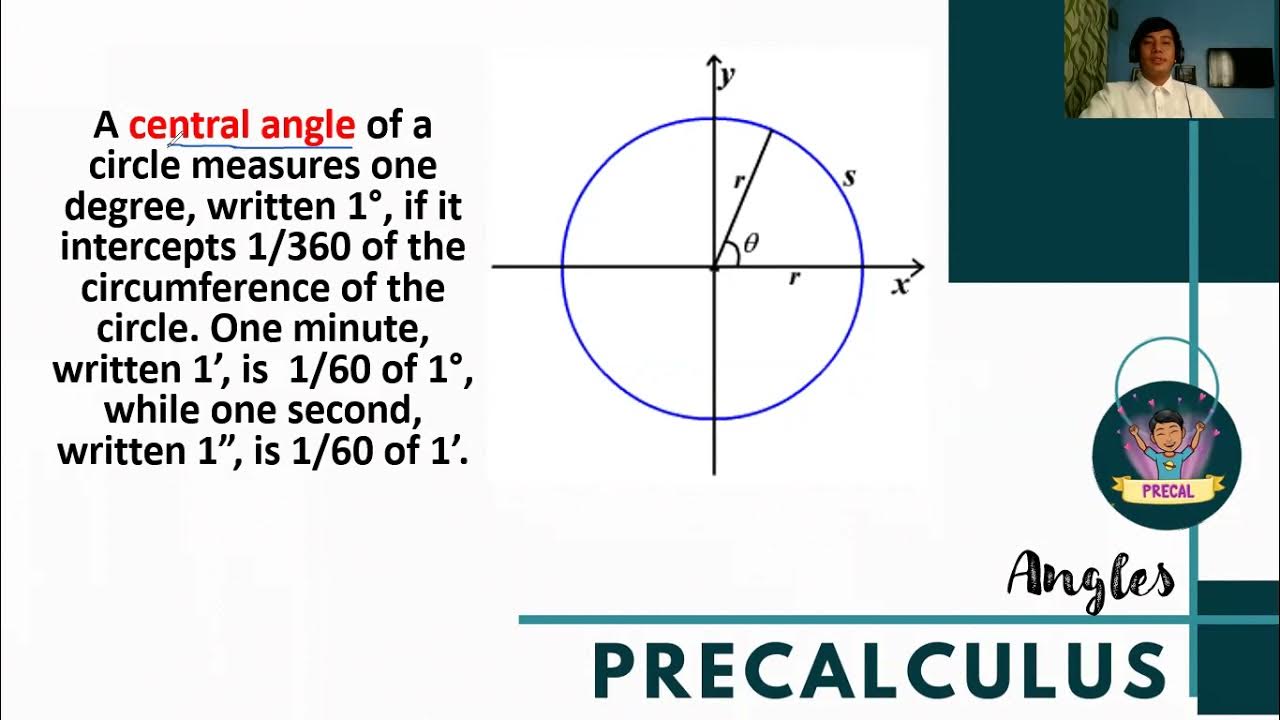
What is the circumference of the unit circle, and how is it calculated?
-The circumference of the unit circle is calculated using the formula C = 2πR. Since the radius R is 1, the circumference is equal to 2π.
What does the Greek letter theta (θ) represent in this context?
-In this context, theta (θ) represents the angle between the positive x-axis and the hypotenuse of a triangle drawn within the unit circle.
How are angles measured in the unit circle, and what is the difference between positive and negative angles?
-Angles in the unit circle are measured in radians, with positive angles measured counterclockwise from the x-axis and negative angles measured clockwise.
What is the relationship between radians and degrees as discussed in the video?
-The video explains that 360 degrees is equivalent to 2π radians, and it demonstrates how to convert angles from radians to degrees and vice versa.
What is the significance of the angle π/4 radians in relation to the unit circle?
-The angle π/4 radians corresponds to 45 degrees and represents a point on the unit circle where the x and y coordinates are equal, specifically √2/2.
How do you derive the values of x and y for the angle π/4 radians?
-For the angle π/4 radians, using the Pythagorean theorem, x² + y² = 1 and knowing that x = y leads to 2x² = 1, giving x = √2/2 and y = √2/2.
What is the approximate decimal value of √2/2 as mentioned in the video?
-The approximate decimal value of √2/2 is about 0.707.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)