ARCOS: MEDIDAS E COMPRIMENTO - GRAU E RADIANO (AULA 1/24)

Summary

This video introduces the basics of trigonometry on the circle, focusing on arcs, angles, and their measurements. The instructor explains the distinction between angular measure and arc length, using both degrees and radians. The relationship between these units is explored, with practical examples on converting between degrees and radians, as well as calculating arc lengths. Additionally, the video emphasizes the formula for the length of an arc and provides exercises to reinforce these concepts. This foundational lesson sets the stage for deeper exploration into the unit circle and trigonometric functions.

Takeaways

• 😀 The course focuses on Trigonometry on the Circle, starting with understanding arcs and the central angle.
• 😀 Arcs are segments of a circle, and the two types are the smaller (blue) and larger (orange) arcs.
• 😀 The smaller arc is typically referred to as 'arc AB' unless otherwise specified.
• 😀 Every arc in a circle determines a central angle, which is formed by drawing two radii to the endpoints of the arc.
• 😀 The measure of an arc refers to its angular measure, while the length of the arc refers to its physical length along the circumference.
• 😀 Two concentric circles (with the same center) can have arcs with the same central angle but different arc lengths due to varying radii.
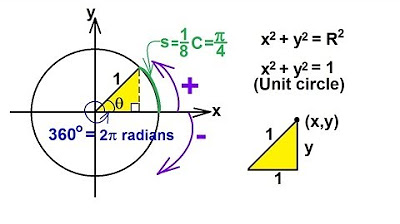
• 😀 The degree measure (360° for a full circle) and the radian measure (2π radians for a full circle) are two units for measuring angles.
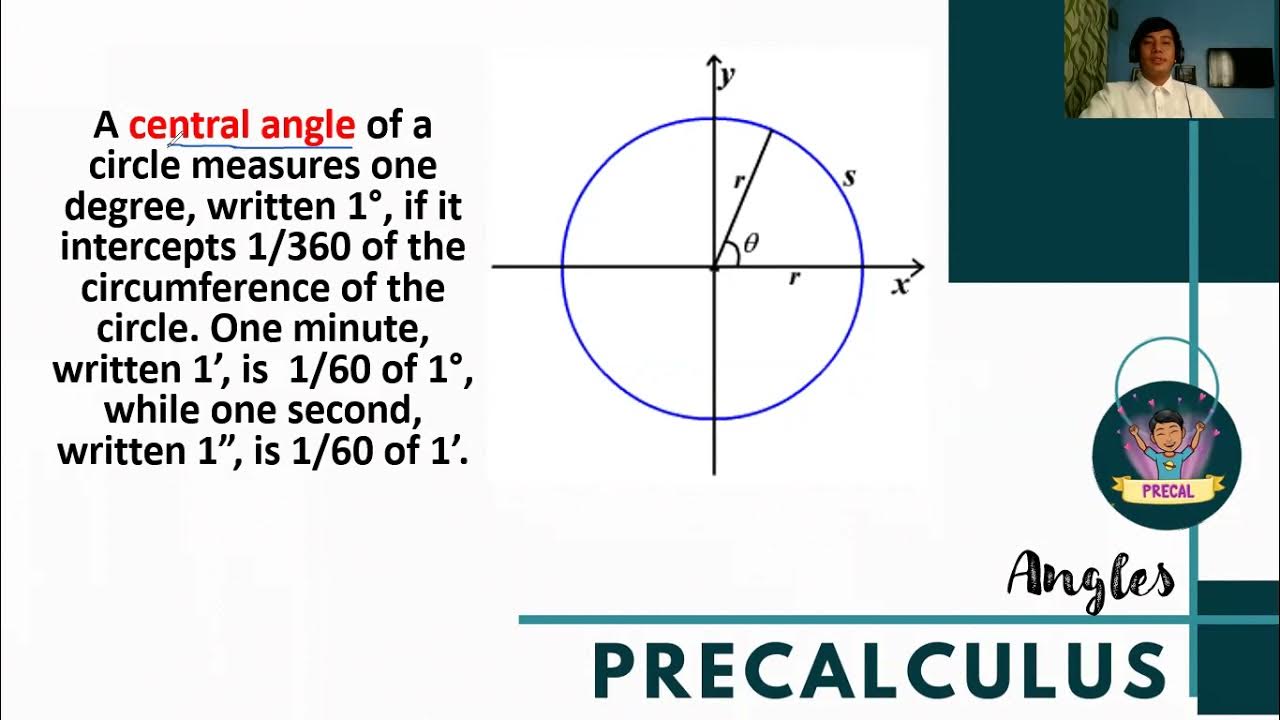
• 😀 1 degree equals 1/360 of a circle, and the radian is defined as the angle subtended by an arc whose length equals the radius.
• 😀 The relationship between degrees and radians is important: 360° equals 2π radians, and 180° equals π radians.
• 😀 The formula to calculate the length of an arc (L) is L = radius × angular measure in radians, where the angular measure (α) is in radians.

Q & A

What is the main topic of the course discussed in the video?

The main topic of the course is Trigonometry on the Circumference, focusing on arcs, central angles, and their measurements.

Why does the instructor emphasize the concept of arcs in the first class?

The instructor emphasizes arcs because they are foundational to understanding trigonometric functions on the circumference, and it's crucial to distinguish between the smaller and larger arcs formed by two points on the circle.

What are the two types of arcs mentioned in the video?

The two types of arcs are the 'smaller arc' and the 'larger arc,' which are formed by two points on the circumference.

How does the central angle relate to the arcs?

The central angle is the angle formed at the center of the circle by two radii connecting to the endpoints of the arc. The size of the central angle corresponds to the measure of the arc.

What is the difference between the 'measure' and 'length' of an arc?

The 'measure' of an arc refers to its angular measure, while the 'length' of an arc refers to its linear distance along the circumference.

What is meant by 'concencentric circles' as mentioned in the video?

Concentric circles are two or more circles that share the same center but have different radii.

What units of measurement are used for angles in the course?

The course uses two units of measurement for angles: degrees and radians.

How is one degree defined in terms of the circumference?

One degree is defined as one 360th of a full circle or a full circumference, which means the circle is divided into 360 equal parts.

What is a radian, and how is it defined?

A radian is the measure of an angle formed when the length of the arc is equal to the radius of the circle. It is a unit of angular measurement used in trigonometry.

What is the relationship between degrees and radians for a full circle?

For a full circle, 360 degrees is equivalent to 2π radians. This establishes the relationship between the two units of measurement.