Matematika SMA - Relasi dan Fungsi (4) - Sifat-Sifat Fungsi, Fungsi Injektif Surjektif (A)

Le GuruLes

27 Oct 202013:05

Summary

TLDRThis educational video script introduces the fundamental properties of functions, focusing on injective, surjective, and bijective functions. It explains the differences through examples and provides a clear method to determine if a function is injective, surjective, or bijective by examining the mapping of elements from the domain to the codomain. The script also includes exercises to test understanding, using sets A and B with various mappings to illustrate the concepts. The video concludes with an invitation to like, share, and subscribe for more educational content.

Takeaways

😀 The video provides an in-depth discussion about the properties of functions, specifically focusing on injective, surjective, and bijective functions.
📚 The presenter encourages viewers to subscribe to the channel and use the notification bell to stay updated with the latest videos on functions.
🔍 The difference between injective, surjective, and bijective functions is explained through their definitions: injective functions map each element of the domain to a unique element in the codomain, surjective functions cover every element in the codomain, and bijective functions are both injective and surjective.
📈 The script includes an example with sets A = {a, b, c, d} and B = {1, 2, 3, 4} to illustrate the concepts of injective, surjective, and bijective functions.
🤔 The video offers a step-by-step guide on how to check if a function is injective, surjective, or bijective by examining the mapping of elements between the domain and codomain.
🚫 It is demonstrated that the function f(x) = x^2 is not injective because different inputs can lead to the same output, violating the definition of an injective function.
📉 The function f(x) = x^2 is also shown not to be surjective because it cannot map to negative outputs, as the square of a real number is always non-negative.
💡 The linear function f(x) = 4x is proven to be injective by showing that different inputs result in different outputs, satisfying the injective condition.
🌐 The same linear function f(x) = 4x is also proven to be surjective, as every element in the codomain has a corresponding element in the domain.
🎯 The conclusion is drawn that f(x) = 4x is bijective because it meets both the injective and surjective criteria.
👍 The video ends with a reminder for viewers to like, share, and subscribe for more educational content, and to follow on Instagram for updates.

Q & A

What are the three types of functions discussed in the video script?
-The three types of functions discussed are injective (one-to-one), surjective (onto), and bijective (one-to-one and onto).
What is an injective function?
-An injective function is a function where every element of the codomain is paired with exactly one element from the domain.
How is a surjective function defined?
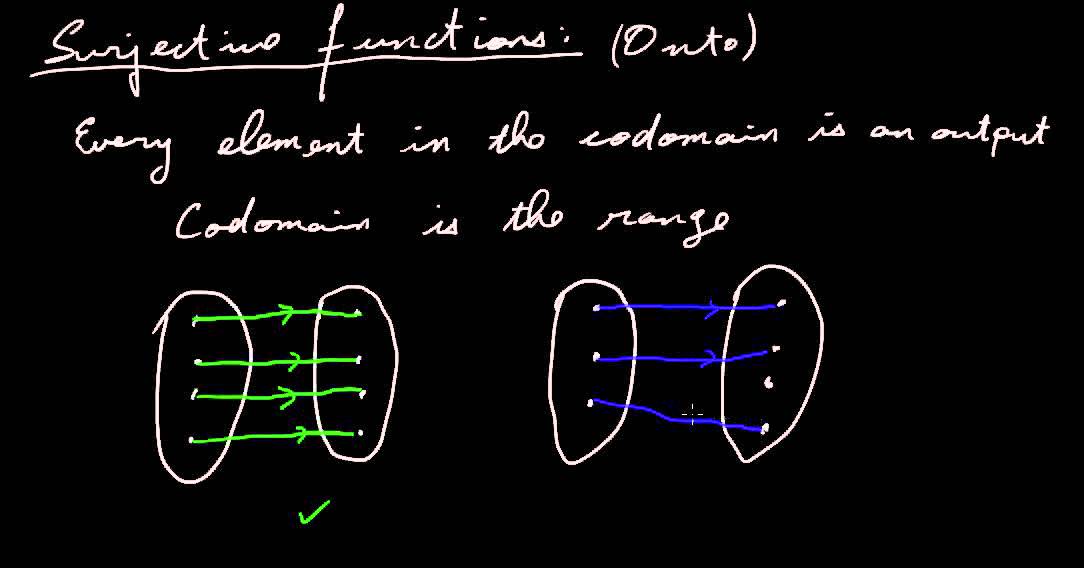
-A surjective function is one where every element of the codomain has at least one corresponding element in the domain.
What is a bijective function?
-A bijective function is one that is both injective and surjective, meaning every element in the domain is paired uniquely with an element in the codomain, and every element in the codomain is the image of some element in the domain.
How can you determine if a function is injective?
-To determine if a function is injective, check if different elements in the domain are mapped to different elements in the codomain, ensuring no two elements in the domain have the same image.
What is the criterion for a function to be surjective?
-A function is surjective if every element in the codomain is the image of at least one element in the domain, meaning the codomain is fully covered by the images of the domain elements.
How do you check if a function is bijective?
-A function is bijective if it is both injective and surjective. This means each element in the domain maps to a unique element in the codomain, and every element in the codomain has a pre-image in the domain.
What is the example function given in the script to illustrate a non-injective function?
-The example function given is f(x) = x^2, which is shown to be non-injective because different values of x (like 2 and -2) can result in the same output (f(2) = f(-2) = 4).
What is the example function provided to demonstrate a surjective function?
-The example function provided is f(x) = 4x, which is surjective because every element in the codomain has a corresponding element in the domain that maps to it.
How is the function f(x) = 4x proven to be injective in the script?
-The function f(x) = 4x is proven to be injective by showing that if x1 ≠ x2, then f(x1) ≠ f(x2), which is demonstrated by choosing specific values for x1 and x2 and showing their images are different.
Why is the function f(x) = x^2 not surjective?
-The function f(x) = x^2 is not surjective because there are elements in the codomain (negative numbers) that do not have a corresponding element in the domain that would map to them, as the square of a real number cannot be negative.
How is the bijectivity of the function f(x) = 4x established in the script?
-The bijectivity of f(x) = 4x is established by proving it is both injective (each domain element maps to a unique codomain element) and surjective (every codomain element has a pre-image in the domain).

Outlines

00:00

📚 Introduction to Function Properties

This paragraph introduces the concept of function properties, specifically focusing on the characteristics of injective (one-to-one), surjective (onto), and bijective (one-to-one correspondence) functions. It explains the differences between these properties using illustrations and provides a basic understanding of how to determine if a function is injective, surjective, or neither by examining the mapping between elements of the domain and codomain. The paragraph also introduces a practice exercise involving the mapping of sets A and B to determine the type of function represented.

05:00

🔍 Analyzing Function Types with Examples

This paragraph delves deeper into analyzing whether a given function is injective, surjective, or bijective by using specific examples. It discusses the criteria for each type of function and applies these to the function f(x) = x^2, demonstrating that it is neither injective nor surjective due to the existence of multiple x values that map to the same y value. The explanation includes a visual representation of the function's graph and the implications of the function's properties on the codomain.

10:00

📉 Examining Linear Functions for Injectivity and Surjectivity

The final paragraph examines the properties of a linear function, f(x) = 4x, to determine if it is injective and surjective. It provides a step-by-step analysis, starting with proving injectivity by showing that different x values result in different f(x) values. The paragraph then moves on to surjectivity, explaining that since every element in the codomain has a corresponding element in the domain, the function is surjective. Finally, it concludes that because the function is both injective and surjective, it is also bijective. The summary ends with a reminder to like, share, and subscribe for more educational content.

Mindmap

Keywords

💡Injective Function

An injective function, also known as a one-to-one function, is a type of function where each element of the domain is mapped to a unique element in the codomain. In the script, the concept is introduced as a fundamental property of functions, and it is used to distinguish it from surjective and bijective functions. The script provides an example to illustrate injective functions, stating that every element in set B is paired with exactly one element from set A, ensuring no two elements in A map to the same element in B.

💡Surjective Function

A surjective function, also called an onto function, is a function where every element of the codomain has at least one corresponding element in the domain. The video script explains surjectivity by stating that all elements in the codomain are accounted for, meaning there are no 'orphaned' elements without a corresponding element in the domain. The script uses the example of a function where every element in set B is mentioned at least once, indicating surjectivity.

💡Bijective Function

A bijective function is a function that is both injective and surjective. It ensures a one-to-one correspondence between the elements of the domain and the codomain. In the script, bijectivity is explained as the union of injective and surjective properties, meaning each element in the codomain is uniquely paired with an element from the domain, and every element in the codomain is accounted for. The script uses visual illustrations to demonstrate bijectivity in the context of set mappings.

💡Domain

The domain of a function refers to the set of all possible inputs for a function. In the script, the domain is the set 'A' which is given as 'abcd' in the example, representing the inputs to the function. The concept is crucial in understanding how functions operate, as it defines the range of values that can be mapped to the codomain.

💡Codomain

The codomain of a function is the set of all possible outputs the function can produce. In the script, the codomain is the set 'B' which is represented as '1 2 3 4'. It is important in the discussion of surjective functions, as it helps determine if every possible output is reached at least once by the function.

💡Function Mapping

Function mapping is the process of assigning outputs to inputs in a function. The script describes function mappings with examples like 'a to 1B, b to 1C, c to 3', illustrating how each element in the domain is associated with an element in the codomain. This concept is central to understanding the properties of functions discussed in the video.

💡Real Numbers

Real numbers are all the numbers that can be represented on the number line, including integers, fractions, and irrational numbers. In the script, the discussion of functions mapping real numbers to real numbers is introduced, with examples of functions like 'f(x) = x squared' and 'f(x) = 4x'. These functions are analyzed for their injectivity, surjectivity, and bijectivity within the context of real numbers.

💡Quadrant

In the context of the script, quadrants refer to the four sections of the Cartesian plane, each defined by a combination of positive and negative x and y coordinates. The script mentions quadrants when discussing the graph of the function 'f(x) = x squared', which is a parabola opening upwards with its vertex at the origin, spanning all quadrants.

💡Graph

A graph is a visual representation of a function, showing the relationship between the input and output values. The script uses the term 'graph' to describe the visual appearance of functions like 'f(x) = x squared' and 'f(x) = 4x', helping to illustrate the properties of injectivity and surjectivity through their shapes and lines on the Cartesian plane.

💡Linear Function

A linear function is a function of the form f(x) = mx + b, where m and b are constants, and x is the input variable. The script refers to a linear function when discussing 'f(x) = 4x', which is a straight line with a slope of 4 on the graph. Linear functions are injective if the slope is not zero and are always surjective, as they cover all possible outputs within the real numbers.

💡Paraboloid

A paraboloid is a three-dimensional surface that resembles a parabola in its shape. In the script, the term is used to describe the graph of 'f(x) = x squared', which opens upwards like a bowl, illustrating the concept of a function that is not injective due to the same output being produced by different inputs.

Highlights

Introduction to the concept of functions and their properties.

Explanation of the three types of functions: injective (one-to-one), surjective (onto), and bijective (one-to-one correspondence).

Description of an injective function where each element of the codomain is paired with exactly one element from the domain.

Illustration of an injective function with an example where some elements in the codomain may not have a pair.

Definition of a surjective function where every element of the codomain has at least one corresponding element from the domain.

Example of a surjective function where all members of the codomain are paired with the domain elements exactly once.

Combination of injective and surjective properties to define a bijective function.

Illustration of a bijective function where each element in the codomain is uniquely paired with an element from the domain.

Introduction to exercises to determine whether given functions are injective, surjective, or bijective.

Method to check if a function is injective by ensuring the codomain elements are mentioned exactly once.

Process to verify if a function is surjective by confirming all codomain elements are accounted for.

Criteria for a function to be bijective: it must be both injective and surjective.

Analysis of a specific function from set A to set B to determine its properties.

Explanation of why the function f(x) = x^2 is not injective due to the mapping of different x values to the same f(x) value.

Demonstration that f(x) = x^2 is not surjective because negative numbers cannot be achieved as outputs.

Conclusion that f(x) = x^2 is neither injective nor surjective, and therefore not bijective.

Introduction of the function f(x) = 4x and its linear graph as an example.

Verification that f(x) = 4x is injective by showing different x values result in different f(x) values.

Confirmation that f(x) = 4x is surjective as every element in the codomain has a corresponding x value in the domain.

Final conclusion that f(x) = 4x is bijective because it is both injective and surjective.

Closing remarks encouraging viewers to like, share, and subscribe for more educational content.