Fungsi #Part 13 // Jenis-jenis Fungsi // Fungsi Modulus // Fungsi Mutlak // Grafik, Domain , Range
Summary
Please replace the link and try again.
Please replace the link and try again.
Please replace the link and try again.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Materi IPS Kelas 9 Bab 4 | Indonesia pada Masa Reformasi Hingga Masa Sekarang

CBSE Class 11 Maths Project-Relations & Functions

Knowing When to Let Go

Apa Itu Massa Jenis Zat
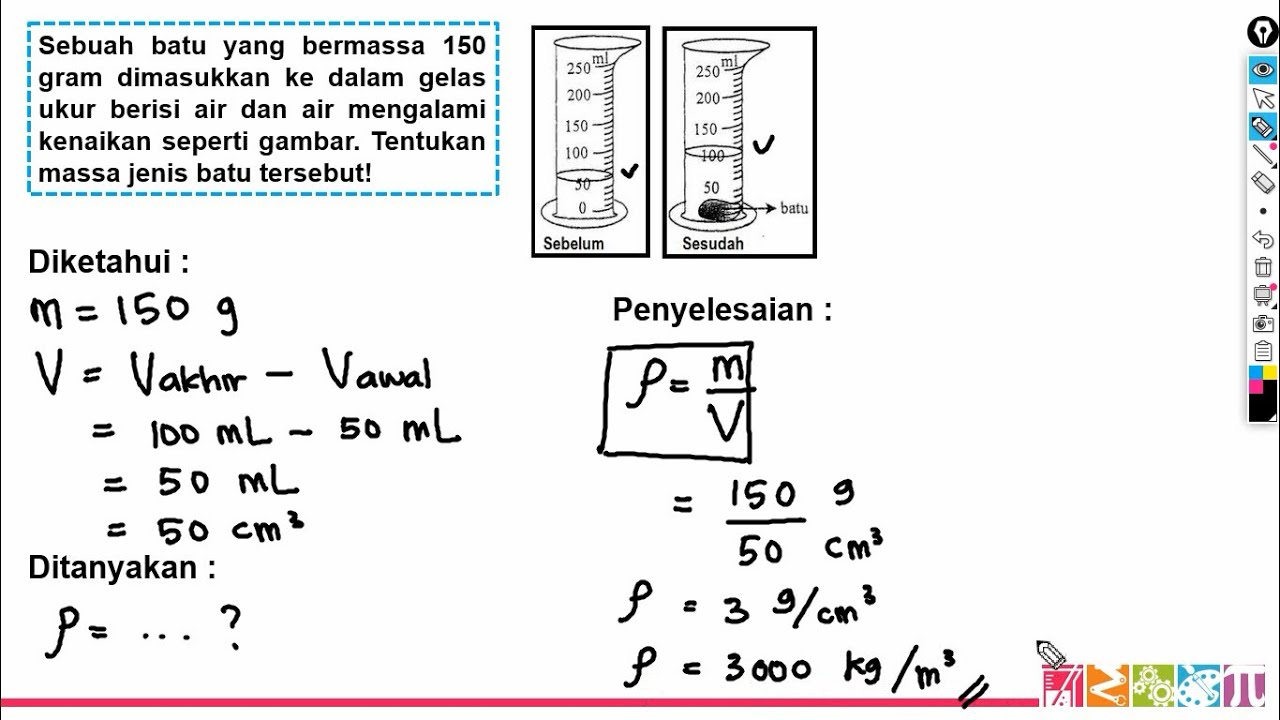
Massa Jenis Benda (IPA SMP)
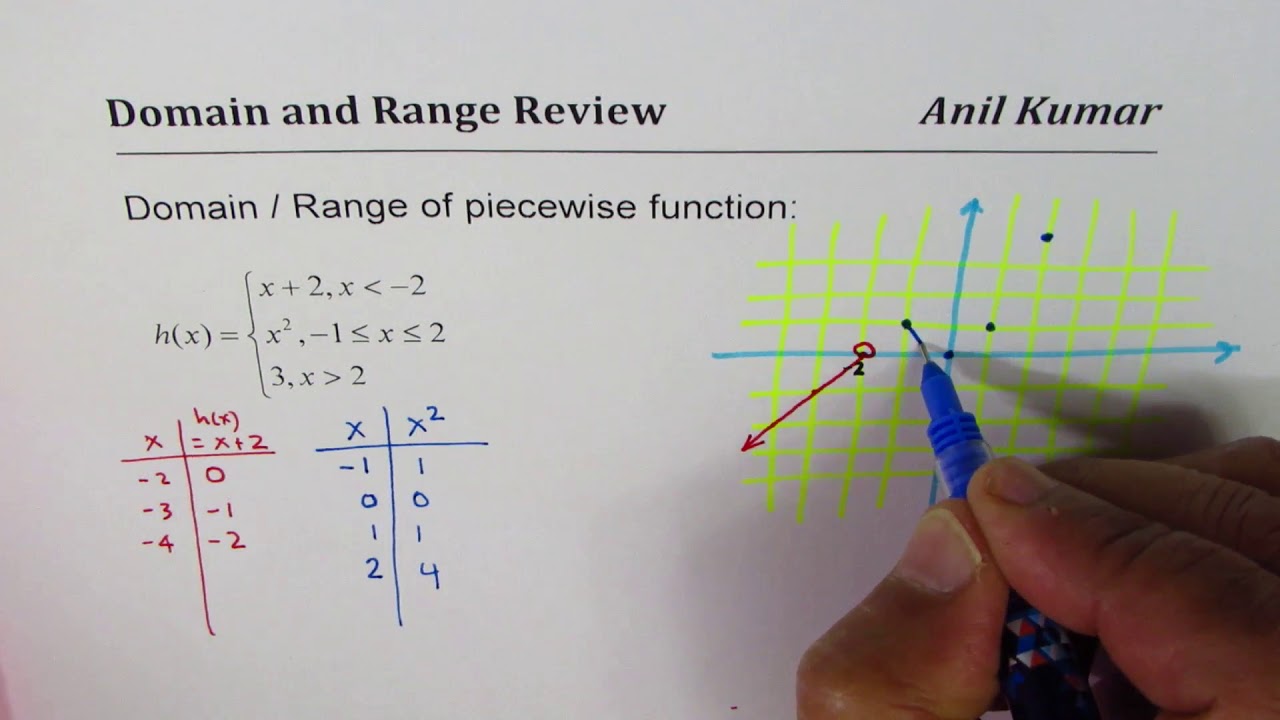
Piecewise Function Domain Range Quadratic Linear Constant

How to find the domain and the range of a function given its graph (example) | Khan Academy
5.0 / 5 (0 votes)