30. Ecuación de la circunferencia con centro en el origen.
Summary
TLDREl video, presentado por Jesús Grajera, explica de forma clara el origen de la ecuación de la circunferencia con centro en el origen. Partiendo de un punto cualquiera sobre la circunferencia forma un triángulo rectángulo y aplica el teorema de Pitágoras para obtener x² + y² = r². Muestra ejercicios: una circunferencia de radio 4 → x² + y² = 16, y la circunferencia que pasa por (3,4) → 3² + 4² = 25 → x² + y² = 25. Grafica los resultados en el programa SMOS, anima al estudiante a entender en vez de memorizar y cierra invitando a suscribirse y seguir sus redes.
Takeaways
- 😀 El objetivo de este tema es enseñar a los estudiantes a determinar la ecuación de un círculo con su centro en el origen.
- 😀 Un círculo es la línea que delimita el círculo, con el centro en el origen representado por el punto (0,0).
- 😀 La ecuación del círculo con centro en el origen proviene del uso del teorema de Pitágoras aplicado a un triángulo rectángulo formado por el radio y las coordenadas de un punto en el círculo.
- 😀 La fórmula que se obtiene a partir del teorema de Pitágoras es: x² + y² = r², donde r es el radio del círculo.
- 😀 Es importante entender cómo surge la ecuación del círculo en lugar de simplemente memorizarla, como ocurre frecuentemente en la educación tradicional.
- 😀 En el ejemplo proporcionado, si el radio del círculo es 4, la ecuación es x² + y² = 16, ya que 4² = 16.
- 😀 La ecuación de un círculo con centro en el origen y radio 4 se puede graficar en un programa como SMOS para visualizar su forma.
- 😀 En otro ejercicio, se encuentra la ecuación de un círculo cuyo centro está en el origen y pasa por el punto (3,4).
- 😀 Para determinar el radio de este círculo, se utiliza nuevamente el teorema de Pitágoras con las coordenadas del punto (3,4): 3² + 4² = 25, por lo que r² = 25.
- 😀 La ecuación final del círculo que pasa por el punto (3,4) es x² + y² = 25, que también se puede graficar para verificar la precisión del resultado.
Q & A
¿Cuál es el objetivo principal de este video?
-El objetivo principal del video es enseñar cómo determinar la ecuación de un círculo con su centro en el origen, explicando de dónde proviene la ecuación y haciendo algunos ejercicios prácticos.
¿Qué es un círculo en términos matemáticos?
-Un círculo es la línea que delimita a la circunferencia, es decir, la línea que encierra todo el círculo. En este caso, el centro está en el origen, en el punto (0,0).
¿Cómo se relacionan las coordenadas (x, y) con el radio del círculo?
-Las coordenadas (x, y) de cualquier punto en la circunferencia permiten aplicar el teorema de Pitágoras para encontrar el radio. El radio se obtiene mediante la suma de los cuadrados de las coordenadas x e y, como r² = x² + y².
¿Cómo se aplica el teorema de Pitágoras en el contexto del círculo?
-En un triángulo rectángulo formado por las coordenadas de un punto en la circunferencia y el origen, el teorema de Pitágoras establece que la suma de los cuadrados de los catetos (x² + y²) es igual al cuadrado de la hipotenusa (r²), que es el radio del círculo.
¿Qué pasa cuando se conoce el radio del círculo?
-Cuando se conoce el radio del círculo, la ecuación del círculo se puede escribir como x² + y² = r², donde r es el radio. Esto permite determinar la ecuación de cualquier círculo con su centro en el origen.
¿Cómo se determina la ecuación de un círculo con un radio dado?
-Para determinar la ecuación de un círculo con un radio dado, basta con sustituir el valor del radio en la fórmula x² + y² = r². Por ejemplo, si el radio es 4, la ecuación será x² + y² = 16.
¿Cómo se resuelve el ejercicio de encontrar la ecuación de un círculo cuyo centro está en el origen y pasa por el punto (3, 4)?
-Para resolver este ejercicio, primero se utiliza el teorema de Pitágoras para calcular el radio, que se obtiene al sumar los cuadrados de las coordenadas del punto: 3² + 4² = 9 + 16 = 25. Luego, se sustituye r² = 25 en la ecuación x² + y² = r², resultando en x² + y² = 25.
¿Qué significa que la ecuación del círculo sea x² + y² = 25 en este caso?
-Significa que el círculo tiene su centro en el origen y su radio es 5, ya que 25 es el cuadrado del radio (r²), por lo que el radio es igual a la raíz cuadrada de 25, es decir, 5.
¿Por qué se usa un programa como SMOS para graficar la ecuación del círculo?
-Se usa un programa como SMOS para graficar la ecuación del círculo porque permite visualizar de manera precisa el círculo generado por la ecuación x² + y² = r², ayudando a confirmar que la solución es correcta al ver la representación gráfica.
¿Qué aprendizaje clave ofrece este video sobre la enseñanza de las matemáticas?
-El aprendizaje clave del video es la importancia de entender el origen de las ecuaciones en lugar de solo memorizarlas. Al comprender de dónde provienen, los estudiantes pueden aplicar los conceptos de manera más efectiva y resolver problemas con mayor confianza.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

32. Ecuación de la circunferencia con centro fuera del origen

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

Ecuación de la circunferencia con centro fuera del origen (cuarta parte)

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN (En su forma ordinaria)

circunferencia que pasa por tres puntos
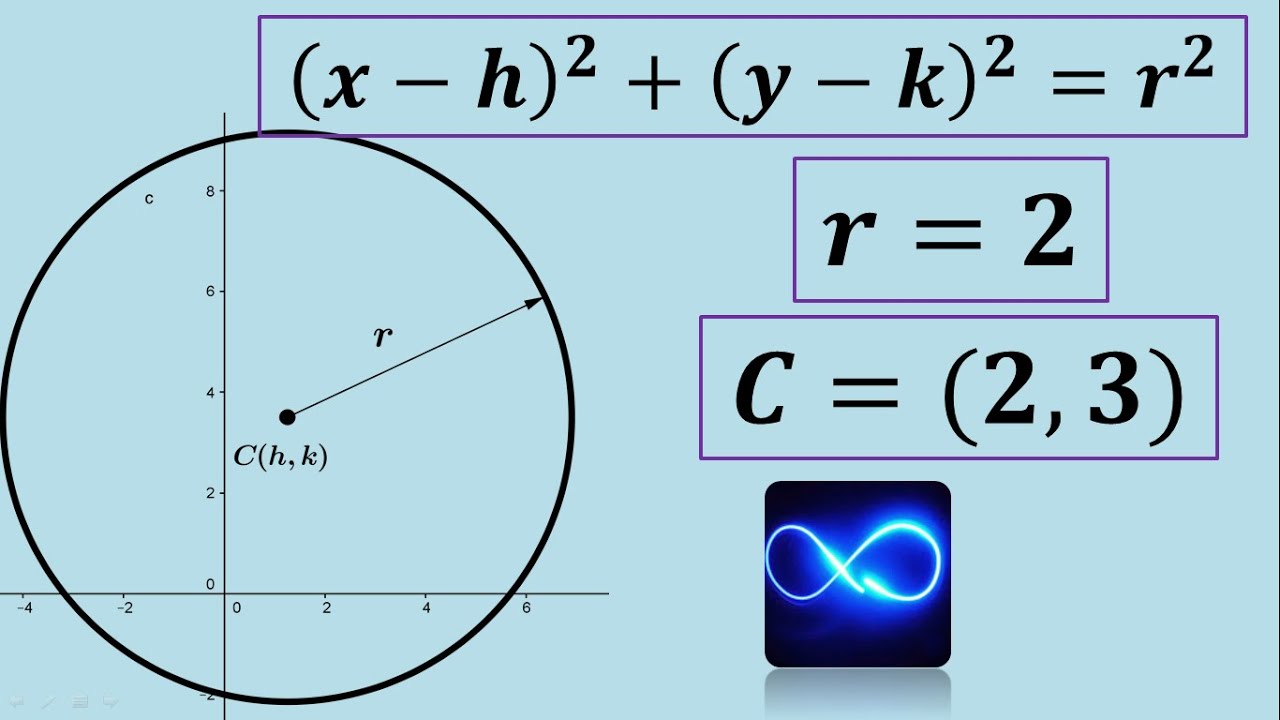
Ordinary and general equation of circumference with given center and radius (Example 1)
5.0 / 5 (0 votes)
