ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN (En su forma ordinaria)

Summary

En este video se aborda el tema de la ecuación de la circunferencia, enfocándose en las formas ordinarias y generales. Se explica cómo determinar la ecuación de una circunferencia cuando su centro está en el origen y también cuando está en otros puntos, usando el valor de 'h' y 'k' del centro. A través de ejercicios prácticos, se muestra cómo obtener la ecuación sustituyendo estos valores y cómo graficar la circunferencia. Además, se incluye una segunda parte para calcular el radio y la ecuación cuando se conocen el centro y un punto de la circunferencia.

Takeaways

• 😀 La ecuación de la circunferencia en su forma ordinaria se puede derivar utilizando el centro (h, k) y el radio (r) de la circunferencia.
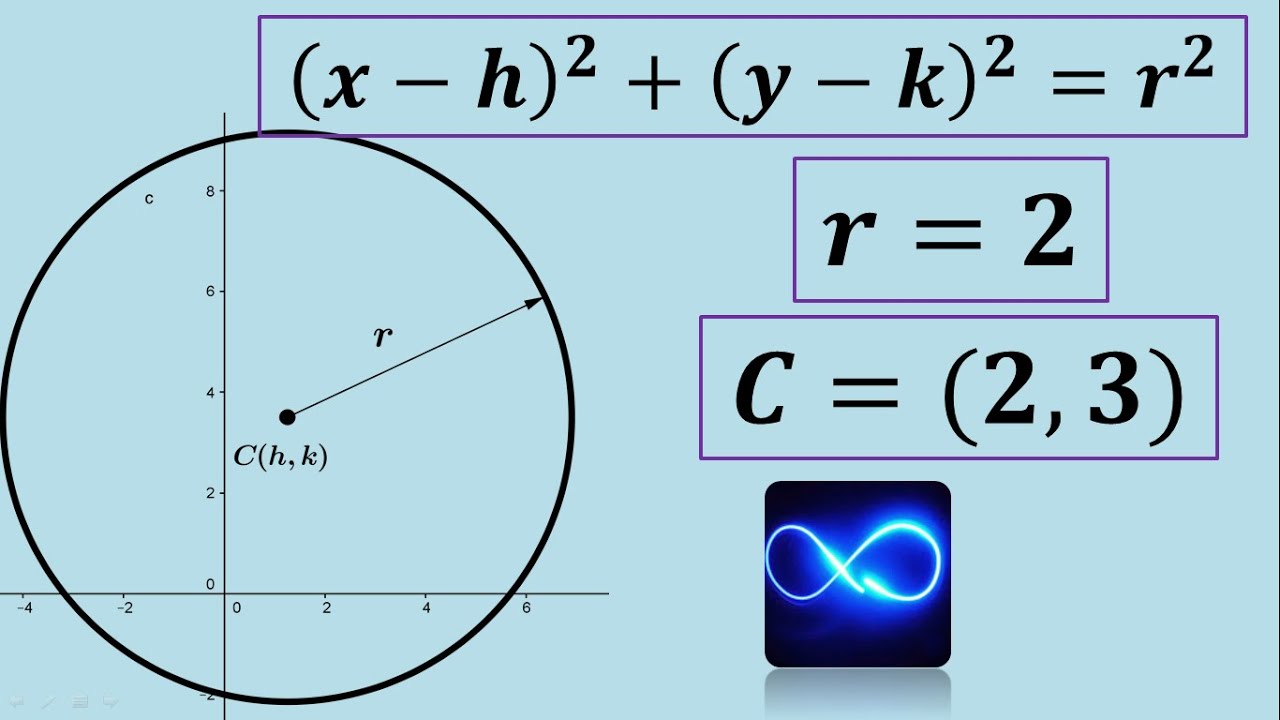
• 😀 La fórmula básica para la ecuación de la circunferencia es (x - h)² + (y - k)² = r², donde h y k son las coordenadas del centro.
• 😀 Es importante identificar correctamente los signos de las coordenadas del centro y del radio cuando se sustituyen en la fórmula.
• 😀 Para graficar la circunferencia, se parte desde el centro (h, k) y se dibujan puntos a una distancia igual al radio r.
• 😀 Un ejercicio de ejemplo mostró cómo sustituir los valores del centro (h = 3, k = -2) y el radio (r = 6) en la ecuación de la circunferencia.
• 😀 En la ecuación de la circunferencia, el signo negativo en la fórmula se convierte en positivo al elevar al cuadrado las coordenadas del centro.
• 😀 Para calcular el radio de una circunferencia cuando no se da explícitamente, se puede usar la distancia entre el centro y un punto sobre la circunferencia.
• 😀 El ejercicio de ejemplo mostró cómo calcular la distancia entre el centro (h = 0, k = -4) y un punto dado (3, 2) para obtener el radio.
• 😀 La distancia entre dos puntos se calcula utilizando el teorema de Pitágoras, sumando los cuadrados de las diferencias en las coordenadas x y y.
• 😀 Al obtener el valor del radio, se sustituye en la fórmula de la circunferencia para obtener su ecuación completa, comprobando que el punto dado está sobre la circunferencia.

Q & A

¿Qué es lo que se va a tratar en este video?

El video trata sobre la ecuación de la circunferencia, específicamente la forma ordinaria de la ecuación cuando el centro está en el origen, y cómo resolver ejercicios con diferentes valores para el centro y el radio.

¿Cuál es la diferencia entre la forma ordinaria y la forma general de la ecuación de la circunferencia?

La forma ordinaria de la ecuación de la circunferencia se utiliza cuando el centro es conocido, y se expresa como (x - h)² + (y - k)² = r². La forma general, en cambio, no está centrada en el origen y puede implicar una ecuación más compleja.

¿Cómo se determina la ecuación de la circunferencia con centro en un punto dado?

Para determinar la ecuación de la circunferencia, se sustituyen los valores de h y k (las coordenadas del centro) y el radio en la fórmula estándar (x - h)² + (y - k)² = r².

En el primer ejercicio, ¿cuál es el centro de la circunferencia?

El centro de la circunferencia es el punto (3, -2), según se indica en el ejercicio.

¿Qué información proporciona el ejercicio para determinar el radio?

El ejercicio indica que el radio de la circunferencia es de 6 unidades.

¿Cómo se calcula la ecuación en el primer ejercicio?

Se sustituye el valor de h (3), k (-2), y el radio (6) en la fórmula estándar. La ecuación resultante es (x - 3)² + (y + 2)² = 36.

En el segundo ejercicio, ¿cuál es el centro de la circunferencia?

El centro de la circunferencia es el punto (0, -4), como se indica en el ejercicio.

¿Cómo se calcula el radio en el segundo ejercicio?

Para calcular el radio, se debe determinar la distancia entre el centro de la circunferencia y el punto por el que pasa la circunferencia. En este caso, la distancia entre (0, -4) y (3, 2) se calcula utilizando el teorema de Pitágoras.

¿Cuál es la fórmula utilizada para calcular la distancia entre dos puntos?

La fórmula para calcular la distancia entre dos puntos (x₁, y₁) y (x₂, y₂) es: √[(x₂ - x₁)² + (y₂ - y₁)²].

¿Qué pasos se siguen para completar la ecuación de la circunferencia en el segundo ejercicio?

Primero, se calcula la distancia entre el centro y el punto (3, 2), que es el radio. Luego, se sustituye el valor de h (0), k (-4) y el radio en la fórmula estándar, resultando en la ecuación (x - 0)² + (y + 4)² = 45.