Ecuación de la circunferencia con centro fuera del origen (cuarta parte)

Summary

En este video se explica cómo obtener la ecuación de una circunferencia cuyo centro no se encuentra en el origen, a partir de la ecuación general. Se aborda el método algebraico de completar cuadrados para transformar la ecuación general en la forma ordinaria, identificando el centro y el radio. Además, se calcula el área y el perímetro del círculo. A lo largo del video, se presentan diversos ejemplos prácticos, mostrando diferentes casos y variantes en la forma de la ecuación, permitiendo que los estudiantes comprendan cómo resolver distintos tipos de problemas relacionados con las circunferencias.

Takeaways

• 😀 La ecuación de la circunferencia con centro fuera del origen se puede expresar de dos maneras: usando fórmulas para el centro y el radio, o mediante una transformación algebraica completando trinomios cuadrados perfectos.
• 😀 Para completar un trinomio cuadrado perfecto, se debe tomar la mitad del coeficiente del término lineal, elevarlo al cuadrado y agregarlo a ambos lados de la ecuación.
• 😀 La ecuación ordinaria de la circunferencia se obtiene transformando la ecuación general a una forma de binomios al cuadrado, lo cual facilita la identificación del centro y el radio.
• 😀 El radio de la circunferencia se puede encontrar como la raíz cuadrada del valor obtenido del lado derecho de la ecuación ordinaria, mientras que el centro se identifica cambiando los signos de los términos en la ecuación.
• 😀 El área encerrada por la circunferencia se calcula como π por el radio al cuadrado, mientras que la longitud (o perímetro) de la circunferencia es 2π por el radio.
• 😀 En el caso de que no haya término lineal en la variable 'x' o 'y', la ecuación se sigue manejando de acuerdo con las mismas reglas algebraicas, pero sin completar trinomios para esas variables.
• 😀 Si la ecuación de la circunferencia no tiene términos lineales ni constantes, el centro puede estar en el origen o en coordenadas específicas basadas en los términos presentes.
• 😀 El procedimiento para resolver estos problemas se puede simplificar al agrupar los términos 'x' y 'y' por separado y luego completar los trinomios cuadrados perfectos para cada uno.
• 😀 La ecuación ordinaria puede tener variaciones, como la ausencia de un término constante o un término lineal, lo que implica diferentes formas en que se puede calcular el centro y el radio de la circunferencia.
• 😀 El cálculo del perímetro de la circunferencia requiere multiplicar 2π por el valor del radio, que se obtiene de la raíz cuadrada del término del lado derecho de la ecuación ordinaria.

Q & A

¿Qué es la ecuación general de una circunferencia?

La ecuación general de una circunferencia es una expresión algebraica que incluye términos cuadráticos y lineales, generalmente escrita como x² + y² + Dx + Ey + F = 0, donde D, E y F son constantes.

¿Cómo se obtiene la ecuación ordinaria de la circunferencia?

Se obtiene transformando la ecuación general en la ecuación ordinaria mediante un procedimiento algebraico, que consiste en completar trinomios cuadrados perfectos. Esto permite reescribir la ecuación de forma que sea más fácil identificar el centro y el radio de la circunferencia.

¿Qué es un trinomio cuadrado perfecto y cómo se completa?

Un trinomio cuadrado perfecto es una expresión algebraica de la forma (a + b)² = a² + 2ab + b². Para completar un trinomio cuadrado perfecto, se toma la mitad del coeficiente del término lineal, se eleva al cuadrado y se añade ese valor al término constante.

¿Por qué se suman los valores que completan el trinomio cuadrado perfecto al lado derecho de la ecuación?

Se suman al lado derecho de la ecuación para mantener el equilibrio y asegurarse de que ambos lados de la ecuación sean iguales. Esto es fundamental en cualquier transformación algebraica.

¿Cómo se encuentra el centro de la circunferencia a partir de la ecuación ordinaria?

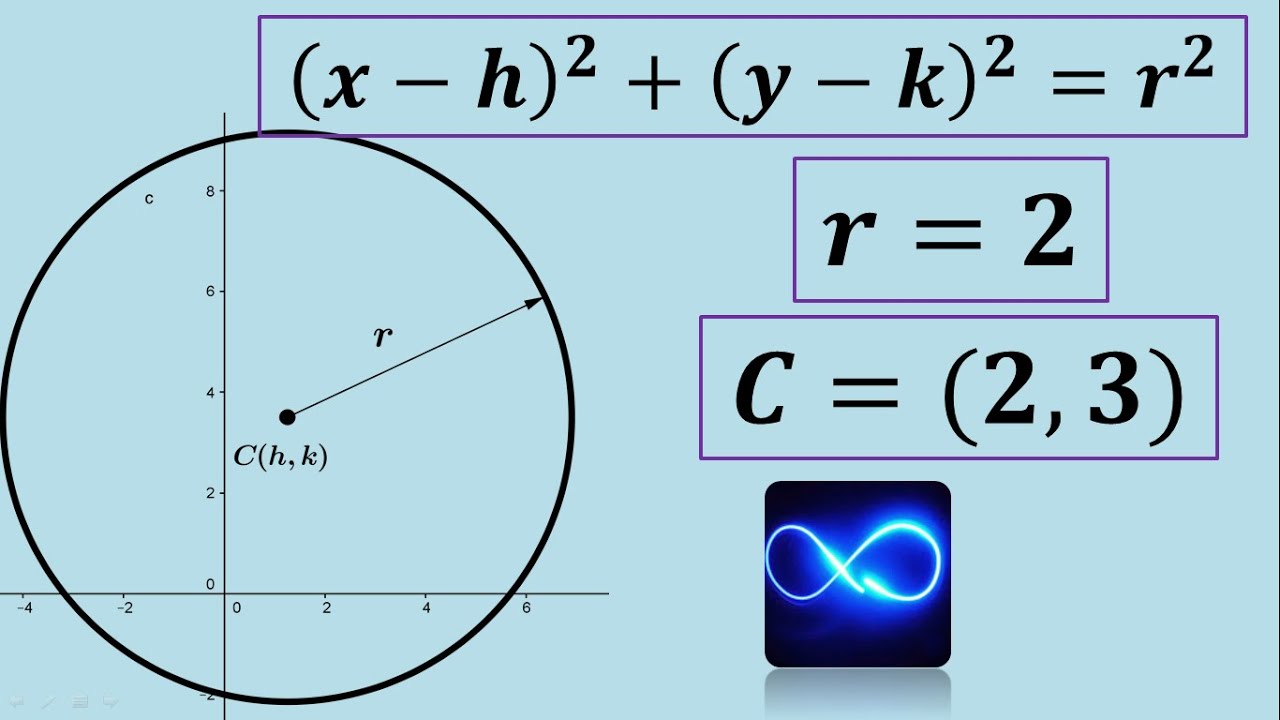
El centro de la circunferencia se encuentra tomando los valores de h y k de la ecuación de la forma (x - h)² + (y - k)² = r², donde h y k son los valores opuestos a los que aparecen en la ecuación transformada. Es decir, si el término es positivo, el valor del centro es negativo y viceversa.

¿Qué representa el radio en la ecuación de la circunferencia?

El radio de la circunferencia es la raíz cuadrada del valor que aparece en el lado derecho de la ecuación ordinaria. Por ejemplo, si la ecuación es (x - h)² + (y - k)² = 16, el radio es la raíz cuadrada de 16, es decir, 4.

¿Cómo se calcula el área de una circunferencia?

El área de una circunferencia se calcula utilizando la fórmula A = πr², donde r es el radio de la circunferencia. Por ejemplo, si el radio es 4, el área sería A = π(4)² = 16π unidades cuadradas.

¿Qué fórmula se utiliza para calcular el perímetro de una circunferencia?

El perímetro (o longitud) de una circunferencia se calcula utilizando la fórmula P = 2πr, donde r es el radio. Si el radio es 4, el perímetro sería P = 2π(4) = 8π unidades.

¿Qué sucede cuando la ecuación general no tiene términos lineales?

Cuando la ecuación general no tiene términos lineales, es decir, no tiene términos de la forma Dx ni Ey, el proceso para completar el trinomio cuadrado perfecto se simplifica, ya que solo hay que trabajar con los términos cuadráticos y constantes.

¿Qué diferencias hay entre los tres ejemplos mostrados en el vídeo?

Los tres ejemplos muestran diferentes variaciones en la ecuación de la circunferencia: en el primer ejemplo, ambos términos lineales están presentes, en el segundo ejemplo falta uno de los términos lineales y en el tercer ejemplo no hay término lineal en x, lo que requiere un enfoque diferente al completar los trinomios cuadrados perfectos.