Ecuación de la circunferencia con centro fuera del origen (tercera parte).
Summary
TLDREn este video, el autor explica cómo encontrar la ecuación de una circunferencia con centro fuera del origen a través de dos métodos: uno utilizando el centro y el radio, y otro mediante la ecuación general. En el primer ejercicio, se determina la ecuación ordinaria y general de una circunferencia dada su longitud. En el segundo ejercicio, se trabaja con tres puntos por los cuales pasa la circunferencia, aplicando un sistema de ecuaciones lineales para encontrar la ecuación general. El video proporciona un análisis detallado de los procedimientos matemáticos y muestra cómo se pueden aplicar fórmulas para obtener la ecuación en ambos casos.
Takeaways
- 😀 El vídeo explica cómo encontrar la ecuación de una circunferencia con centro fuera del origen y diferentes condiciones iniciales.
- 😀 El primer ejercicio utiliza el centro (-3, 1) y el perímetro de 14π para encontrar la ecuación ordinaria y general de la circunferencia.
- 😀 La fórmula para calcular el perímetro de una circunferencia es 2πr, y se usa para encontrar el radio, que en este caso es 7.
- 😀 La ecuación ordinaria de la circunferencia se obtiene utilizando el centro y el radio, y se expresa como (x + 3)² + (y - 1)² = 49.
- 😀 Para encontrar la ecuación general, se utilizan fórmulas donde 'd' es igual a -2h, 'e' es igual a -2k, y 'f' se calcula usando los valores del centro y radio.
- 😀 En el segundo ejercicio, se parte de tres puntos dados (A, B y C) por los que pasa la circunferencia para encontrar la ecuación general directamente.
- 😀 La ecuación general de una circunferencia tiene términos cuadráticos y lineales en x y y, y se utiliza para resolver sistemas de ecuaciones con tres incógnitas.
- 😀 Se resuelven sistemas de ecuaciones lineales con tres incógnitas para encontrar los valores de 'd', 'e' y 'f', y así obtener la ecuación general de la circunferencia.
- 😀 Para simplificar el sistema de ecuaciones, se multiplican las ecuaciones por constantes y se utilizan métodos de suma y resta para eliminar incógnitas.
- 😀 Al final del proceso, se obtiene la ecuación general de la circunferencia, y a partir de ella, se puede calcular el centro y el radio de la circunferencia.
- 😀 El centro de la circunferencia se obtiene de la forma general, utilizando las fórmulas 'd = -2h' y 'e = -2k', y el radio se encuentra a partir de la relación entre 'f', 'h' y 'k'.
Q & A
¿Qué información nos dan en el primer ejercicio del video?
-En el primer ejercicio, se nos da el centro de la circunferencia, que está en (-3, 1), y la longitud de la circunferencia, que es 14π. A partir de esto, se calcula el radio y se obtiene la ecuación ordinaria de la circunferencia.
¿Cómo se calcula el radio de la circunferencia en el primer ejercicio?
-El radio se calcula usando la fórmula del perímetro de la circunferencia: 2πr = 14π. Despejando r, se obtiene que r = 7.
¿Cuál es la ecuación ordinaria de la circunferencia en el primer ejercicio?
-La ecuación ordinaria de la circunferencia es: (x + 3)² + (y - 1)² = 49.
¿Cómo se obtiene la ecuación general de la circunferencia?
-Para obtener la ecuación general, se utilizan fórmulas específicas que involucran los valores de h, k y f. Al sustituir los valores obtenidos en el ejercicio, se obtiene la ecuación general: x² + y² + 6x - 2y - 39 = 0.
¿Qué se necesita para resolver el segundo ejercicio?
-En el segundo ejercicio, se nos dan tres puntos por los que pasa la circunferencia. No se conoce el centro ni el radio, por lo que se deben calcular esos valores o directamente la ecuación general de la circunferencia.
¿Cómo se resuelve el segundo ejercicio si no se tiene el centro ni el radio?
-En este caso, se puede resolver utilizando un sistema de ecuaciones para encontrar los valores de las constantes D, E y F en la ecuación general de la circunferencia. Después de esto, se puede encontrar el centro y el radio si se desea.
¿Qué pasos se siguen para obtener la ecuación general en el segundo ejercicio?
-Se sustituyen las coordenadas de los tres puntos en la ecuación general de la circunferencia y se obtienen tres ecuaciones lineales con tres incógnitas. Luego, se resuelven simultáneamente para obtener los valores de D, E y F.
¿Cómo se resuelve el sistema de ecuaciones en el segundo ejercicio?
-Se utilizan métodos como la suma y resta de ecuaciones para eliminar incógnitas y reducir el sistema a una ecuación con menos incógnitas. Luego, se repiten estos pasos hasta encontrar los valores de D, E y F.
¿Cuál es la ecuación general resultante en el segundo ejercicio?
-La ecuación general resultante es: x² + y² + 6x - 6y - 47 = 0.
¿Cómo se obtiene el centro y el radio de la circunferencia a partir de la ecuación general?
-A partir de la ecuación general, se pueden utilizar las fórmulas para encontrar el centro y el radio. El centro es (-3, 3) y el radio es √65, que equivale aproximadamente a 8.04.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Encontrar el centro y radio de la CIRCUNFERENCIA conociendo la ecuación general EJEMPLO 2
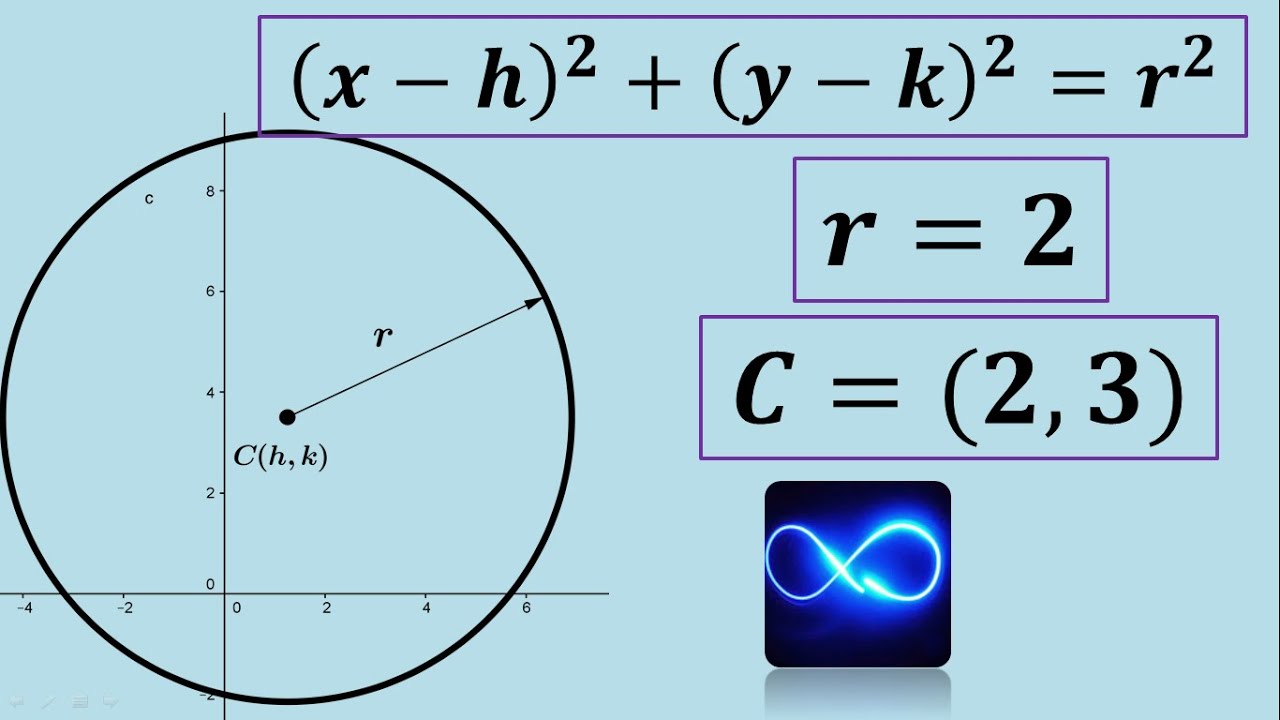
Ordinary and general equation of circumference with given center and radius (Example 1)

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN (En su forma ordinaria)

32. Ecuación de la circunferencia con centro fuera del origen

Ecuación de la circunferencia con centro fuera del origen (cuarta parte)

Find center and radius of circumference (completing perfect square trinomial)
5.0 / 5 (0 votes)
